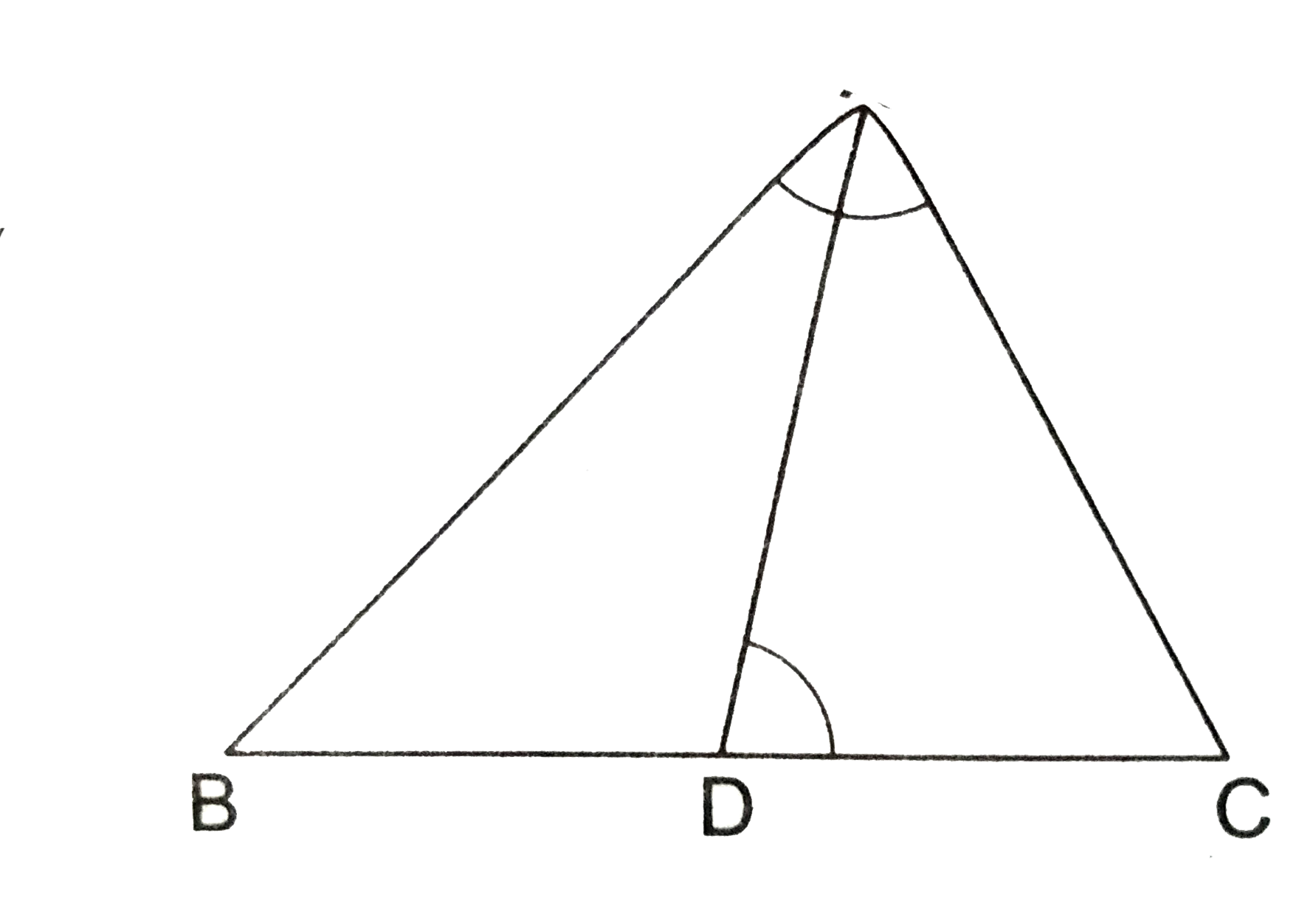
Let O be the in-centre of a triangle ABC and D be a point on the side BC of $Δ A B C$ , such that $O D ⊥ B C$ If $∠ B O D = 15^{\circ}$ , then $∠ A B C = ?$

$75^{\circ}$

$45^{\circ}$

$150^{\circ}$

$90^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video, text & image solution for Let O be the in-centre of a triangle ABC and D be a point on the side BC of Delta ABC, such that OD_|_BC If angle BOD=15^(@), then angle ABC=? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.

Updated on:21/07/2023

Class 14 MATHS GEOMETRY

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Let O be the in-centre of a triangle ABC and D be a point on the side BC of $Δ A B C$ , such that $O D ⊥ B C$ If $∠ B O D = 15^{\circ}$ , then $∠ A B C = ?$
A $75^{\circ}$
B $45^{\circ}$
C $150^{\circ}$
D $90^{\circ}$
Question 2 - Select One
If D is a Point on the side BC of a $Δ A B C$ such that AD bisects $∠ B A C$ . Then
ABD=CD
B $B A > B D$
C $B D > B A$
D $C D < C A$
Question 3 - Select One
Let 'l' is the length of median from the vertex A to the side BC of a $Δ A B C$ . Then
A $4 l^{2} = 2 b^{2} + 2 c^{2} - a^{2}$
B $4 l^{2} = b^{2} + c^{2} + 2 b c cos A$
C $4 l^{2} = a^{2} + 4 b c cos A$
D $4 l^{2} = {(2 s - a)}^{2} {sin}^{2} \frac{A}{2}$

KIRAN PUBLICATION-GEOMETRY-QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)

Home
Ask Doubt
Profile

Let O be the in-centre of a triangle ABC and D be a point on the side BC of ΔABC, such that OD⊥BC If ∠BOD=15∘, then ∠ABC=?

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let O be the in-centre of a triangle ABC and D be a point on the side BC of ΔABC, such that OD⊥BC If ∠BOD=15∘, then ∠ABC=?

If D is a Point on the side BC of a ΔABC such that AD bisects ∠BAC. Then

Let 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then

KIRAN PUBLICATION-GEOMETRY-QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)

Let O be the in-centre of a triangle ABC and D be a point on the side BC of $Δ A B C$ , such that $O D ⊥ B C$ If $∠ B O D = 15^{\circ}$ , then $∠ A B C = ?$

Let O be the in-centre of a triangle ABC and D be a point on the side BC of $Δ A B C$ , such that $O D ⊥ B C$ If $∠ B O D = 15^{\circ}$ , then $∠ A B C = ?$

If D is a Point on the side BC of a $Δ A B C$ such that AD bisects $∠ B A C$ . Then

Let 'l' is the length of median from the vertex A to the side BC of a $Δ A B C$ . Then