In ΔABC,PQ is parallel to BC. If AP:PB=1:2and AQ=3cm, AC is equal to
6 cm
9 cm
12 cm
8 cm
The correct Answer is:B
To solve the problem step by step, we will use the Basic Proportionality Theorem (also known as Thales' theorem).
Step 1: Understand the given information
We have triangle ABC with a line PQ parallel to side BC. The ratio of segments AP to PB is given as 1:2, and the length of segment AQ is given as 3 cm.
Step 2: Set up the ratio
According to the Basic Proportionality Theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Therefore, we can write the following ratio based on the given information:
APPB=AQQC
Given that AP:PB=1:2, we can express this as:
12=AQQC
Step 3: Substitute the known value
We know that AQ=3cm. We can substitute this value into the ratio:
12=3QC
Step 4: Solve for QC
To find QC, we can cross-multiply:
1⋅QC=2⋅3
QC=6cm
Step 5: Find the length of AC
Now that we have both AQ and QC, we can find the total length of AC:
AC=AQ+QC=3cm+6cm=9cm
Final Answer
Thus, the length of AC is 9cm.
---
We have triangle ABC with a line PQ parallel to side BC. The ratio of segments AP to PB is given as 1:2, and the length of segment AQ is given as 3 cm.
According to the Basic Proportionality Theorem, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Therefore, we can write the following ratio based on the given information:
We know that AQ=3cm. We can substitute this value into the ratio:
To find QC, we can cross-multiply:
QC=6cm
Now that we have both AQ and QC, we can find the total length of AC:
Thus, the length of AC is 9cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)35videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)30videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
In a △ABC, DE is parallel to BC, AD = 3 cm, AE = 4cm and AC = 10 cm, then the value of BD in centimetres, is:
△ABC में, DE, BC & समानांतर है, AD = 3 cm, AE= 4cm और AC = 10 cm, फिर BD (सेंटीमीटर में) मान है:View SolutionIn ΔABC, PQ is parallel to BC, while P and Q are at AB and AC respectively. If AB = 3AP, then what is the ratio of areas of triangles ΔAPQ and ΔABC.
View Solution
Knowledge Check
- Question 1 - Select One
D and E are points on sides AB and AC of ΔABC. DE is parallel to BC. If AD : DB = 1 : 2 and area of ΔABC is 45 sq. cm., what is the area (in sq. cm.) of quadrilateral BDEC ?
A20B40C15D30 - Question 2 - Select One
Points P and Q lie on the sides AB and AC of triangle ABC respectivey such that line segment PQ is parallel to side BC. If the ratio of AP : PB is 1 : 4 and area of ΔAPQ is 4 square cm., what is the area of trapezium PQCB ?
A60 sq. cmB16 sq. cmC96 sq. cmD21 sq. cm - Question 3 - Select One
In ΔABC, the line parallel to BC Intersects AB and AC at P and Q respectively. If AB:AP=5:3then AQ:QCis :
A3:2B2:3C3:5D1:2
In ΔABCandΔEDC,AB is parallel to ED.BD=13BCandAB=12.3cm
View SolutionLet D, E be the points on sides AB and AC respectively of a triangle ABC such that DE is parallel to BC. Let AD = 2 cm, DB = 1 cm, AE = 3 cm and area of triangle ADE = 3 cm2 What is EC equal to ?
View SolutionIn the figure given below, ABC is an equilateral triangle with each side of length 30 cm. XY is parallel to BC, XP is parallel to AC and YQ is parallel to AB. If XY + XP + YQ is 40 cm, then the value of PQ is
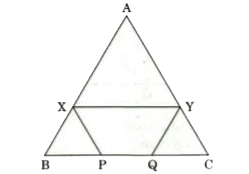 View Solution
View SolutionΔABC is right-angled at A and AD⊥BC. If BC=13cmandAC=5cm, find the ratio of areas of ΔABCandΔADC.
 View Solution
View SolutionIn a ΔABC, if DE is drawn parallel to BC, cutting AB and AC to D and E respectively such that AB=7.2cm,AC=6.4cmandAD=4.5cm. Then, AE=?
 View Solution
View Solution

