The external bisector of ∠Band∠C of ΔABC(where AB and AC extended to E and F respectively) meet at point P. If ∠BAC=100∘, then the measure of ∠BPC is
50∘
80∘
40∘
100∘
The correct Answer is:C
To solve the problem, we need to find the measure of angle ∠BPC given that ∠BAC=100∘. We will use the property of external angle bisectors.
1. Identify the Given Information:
- We have triangle ABC.
- The external bisectors of angles B and C meet at point P.
- The measure of angle A (i.e., ∠BAC) is given as 100∘.
2. Use the External Angle Bisector Theorem:
- The theorem states that the measure of the angle formed by the external bisectors of angles B and C at point P can be calculated using the formula:
∠BPC=90∘−∠A2
3. Substitute the Given Angle:
- We know ∠A=100∘.
- Therefore, we substitute ∠A into the formula:
∠BPC=90∘−100∘2
4. Calculate 100∘2:
- This simplifies to:
100∘2=50∘
5. Final Calculation:
- Now substitute 50∘ back into the equation:
∠BPC=90∘−50∘=40∘
6. Conclusion:
- Thus, the measure of ∠BPC is 40∘.
Final Answer:
∠BPC=40∘
- We have triangle ABC.
- The external bisectors of angles B and C meet at point P.
- The measure of angle A (i.e., ∠BAC) is given as 100∘.
- The theorem states that the measure of the angle formed by the external bisectors of angles B and C at point P can be calculated using the formula:
∠BPC=90∘−∠A2
- We know ∠A=100∘.
- Therefore, we substitute ∠A into the formula:
∠BPC=90∘−100∘2
- This simplifies to:
100∘2=50∘
- Now substitute 50∘ back into the equation:
∠BPC=90∘−50∘=40∘
- Thus, the measure of ∠BPC is 40∘.
∠BPC=40∘
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)35videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)30videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC, draw BE⊥ACand CF⊥AB and the perpendicular BE and CF Intersect at the point O. If ∠BAC=70∘, then the value of ∠BOCis
A125∘B55∘C150∘D110∘ - Question 2 - Select One
In a △ABC, the bisectors of ∠B and ∠C meets at point O inside the triangle. If ∠BOC=122∘, then the measure of ∠A
△ABCमें, ∠B तथा ∠C द्विभाजक त्रिभुज के भीतर बिंदु O पर मिलते हैं | यदि ∠BOC=122∘ है, तो ∠A का माप क्या होगा ?A64∘B62∘C72∘D68∘ - Question 3 - Select One
Internal bisectors of angles ∠Band∠C of a triangle ABC meet at O. If ∠BAC=80∘, then the value of ∠BOC is
A120∘B140∘C110∘D130∘
In Fig. 7.48, sides ABandAC of ΔABC are extended to points PandQ respectively. Also, ∠PBC <∠QCB. Show that AC > AB.
 View Solution
View SolutionAn exterior angle of a triangle is 1100 , and one of the interior opposite angles is 300. Find the other two angles of the triangle.
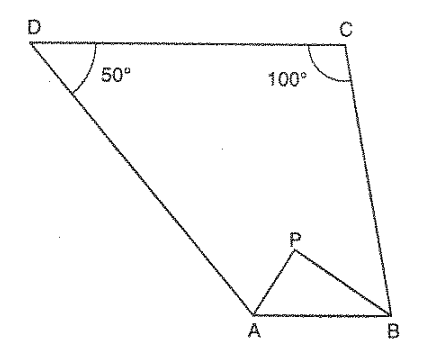
View SolutionIn Figure, the bisectors of ∠A and ∠B meet at a point P. If ∠C=1000 and ∠D=500, find the measure of ∠APB
 View Solution
View SolutionAD is a median of △ABC. The bisectors of ∠ADBand∠ADC meets AB and AC in E and F respectively prove that EF||BC.
View SolutionIn △ABC, if AB=AC and ∠BAC=40∘ ,then the measure of ∠B is
त्रिभुज ABC में, यदि AB=AC है तथा ∠BAC=40∘ है, तो कोण B का मान क्या होगा ?View Solution


