In ΔABC,AB=AC,Ois a point on BC such that BO = CO and OD is perpendicular to AB and OE is perpendicular to AC. If ∠BOD=30∘ then measure of ∠AOE is
45∘
60∘
75∘
30∘
The correct Answer is:B
To solve the problem, we need to analyze the given information about triangle ABC and the points O, D, and E.
1. Identify the Triangle and Points:
- We have triangle ABC where AB = AC (isosceles triangle).
- Point O is on line segment BC such that BO = CO, meaning O is the midpoint of BC.
- OD is perpendicular to AB, and OE is perpendicular to AC.
2. Understanding Angles:
- Given that angle BOD = 30 degrees, we need to find angle AOE.
3. Using Properties of Isosceles Triangle:
- Since triangle ABC is isosceles with AB = AC, angles ABC and ACB are equal. Let's denote these angles as x.
- The vertex angle A (angle BAC) can be expressed as:
∠A=180∘−2x
4. Analyzing Triangle BOD:
- In triangle BOD, we know:
- Angle BOD = 30 degrees
- Angle OBD = 90 degrees (since OD is perpendicular to AB)
- Therefore, angle ODB can be calculated as:
∠ODB=180∘−∠BOD−∠OBD=180∘−30∘−90∘=60∘
5. Finding Angle AOE:
- Since OE is perpendicular to AC, angle OEA is also 90 degrees.
- In triangle AOE, we can find angle AOE using the fact that the angles in a triangle sum up to 180 degrees:
∠AOE+∠OAE+∠OEA=180∘
- We know that angle OEA = 90 degrees and angle OAE = angle ODB = 60 degrees (from step 4).
- Thus, we have:
∠AOE+60∘+90∘=180∘
- Simplifying this gives:
∠AOE+150∘=180∘
- Therefore:
∠AOE=180∘−150∘=30∘
Final Answer:
The measure of angle AOE is 30 degrees.
- We have triangle ABC where AB = AC (isosceles triangle).
- Point O is on line segment BC such that BO = CO, meaning O is the midpoint of BC.
- OD is perpendicular to AB, and OE is perpendicular to AC.
- Given that angle BOD = 30 degrees, we need to find angle AOE.
- Since triangle ABC is isosceles with AB = AC, angles ABC and ACB are equal. Let's denote these angles as x.
- The vertex angle A (angle BAC) can be expressed as:
∠A=180∘−2x
- In triangle BOD, we know:
- Angle BOD = 30 degrees
- Angle OBD = 90 degrees (since OD is perpendicular to AB)
- Therefore, angle ODB can be calculated as:
∠ODB=180∘−∠BOD−∠OBD=180∘−30∘−90∘=60∘
- Since OE is perpendicular to AC, angle OEA is also 90 degrees.
- In triangle AOE, we can find angle AOE using the fact that the angles in a triangle sum up to 180 degrees:
∠AOE+∠OAE+∠OEA=180∘
- We know that angle OEA = 90 degrees and angle OAE = angle ODB = 60 degrees (from step 4).
- Thus, we have:
∠AOE+60∘+90∘=180∘
- Simplifying this gives:
∠AOE+150∘=180∘
- Therefore:
∠AOE=180∘−150∘=30∘
The measure of angle AOE is 30 degrees.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)35videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)30videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
In ΔABC, AB=AC and D is a point on side AC such that BD = BC, If AB = 12.5 cm and BC = 5 cm, then what is the measure of DC ?
A2 cmB2.5 cmC3 cmD1.8 cm - Question 2 - Select One
In ΔABC,BDandCEareperpendica––r→ACandABrespectively.IfBD = CE,thenDelta ABC is
AEquilateralBIsoscelesCRight-angledDScalene - Question 3 - Select One
If D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
Aa2+b2+c2=4b2Ba2+b2−c2=4b2Ca2−b2+c2=4b2Da2−b2−c2=4b2
In triangle ABC,D is the midpoint of BC and AD is perpendicular to AC. Then cosA.cosC=
View SolutionIf D is a point of the base BC of an isosceles triangle ABC such that AD is perpendicular to AC, then a=
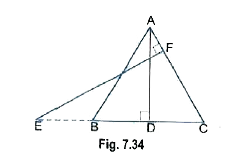
View SolutionIn the given Fig. 7 .34, AB = AC. E is a point on CB produced. If AD is perpendicular to BC and EF perpendicular to AC, prove that ΔABD is similar to ΔCEF.
 View Solution
View SolutionAB is a straight line, C and D are points on the same side of AB such that AC is perpendicular to AB and DB is perpendicular to AB. Let AD and BC meet at E.
What is AEAD+DEBC equal to ?View SolutionIn a triangle ABC, ∠BAC=90∘, AD is the altitude from A on to BC. Draw DE perpendicular to AC and DF perpendicular to AB. Suppose AB =15 and BC = 25. Then the length of EF is
View Solution

