Question

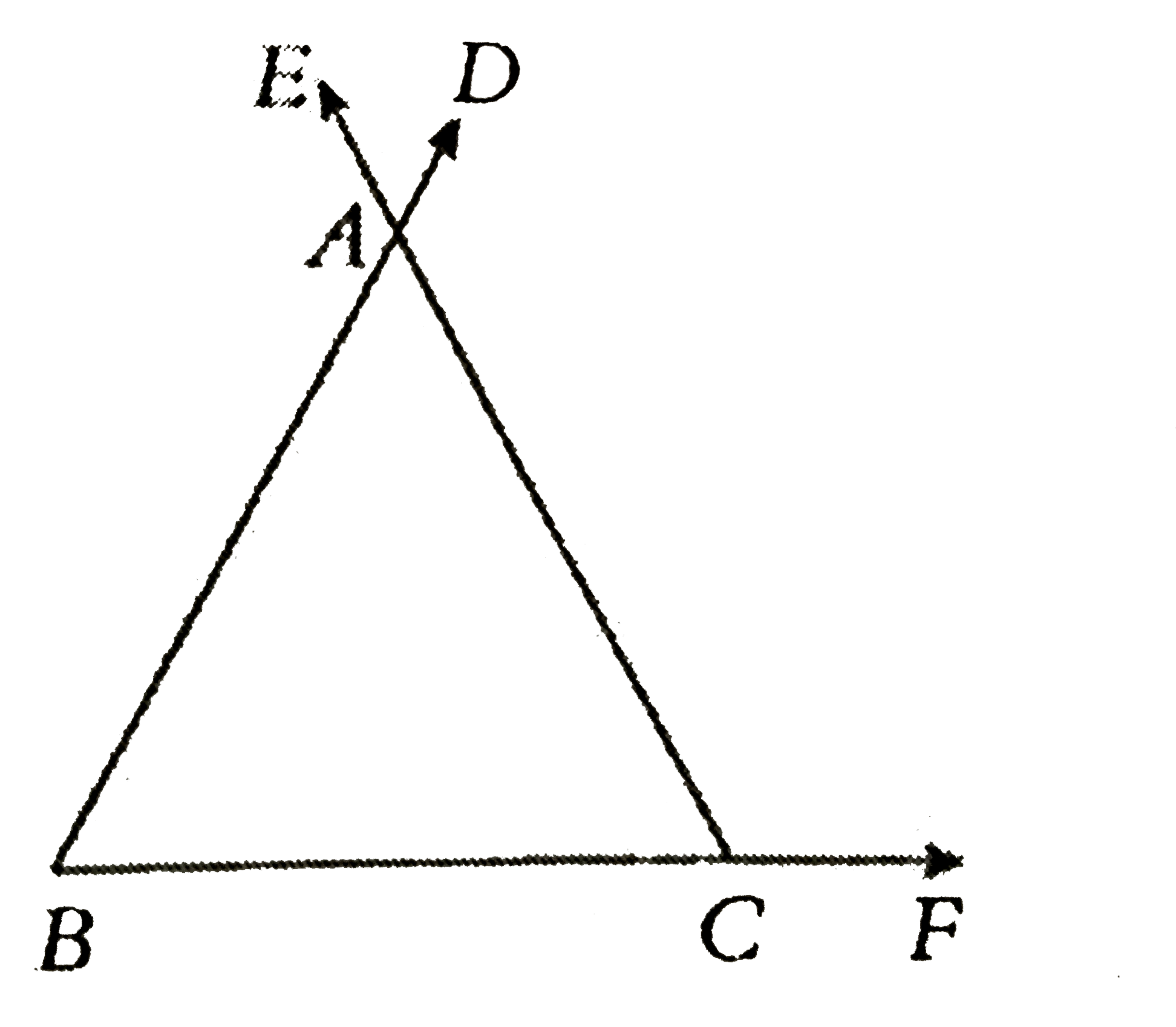
ABC is a triangle and the sides AB, BC and CA are produced to E, F and G respectively. If $\angle CBE=\angle ACF={130}^{\circ }$ then the value of $\angle GAB$ is

Options

A. `100^@`
B. `130^@`
C. `80^@`
D. `90^@`

Answer

A

Explanation

To solve the problem step by step, we will analyze the triangle ABC and the angles given.

Step 1: Understand the Triangle and Given Angles
We have triangle ABC with sides extended to points E, F, and G. We know:
- Angle CBE = 130°
- Angle ACF = 130°

Step 2: Identify Angles X and Y
Let:
- Angle GAB = X
- Angle ABC = Y

Step 3: Apply Linear Pair on Angle CBE
Since angle CBE and angle GAB (X) are on a straight line:
\( X + \text{Angle CBE} = 180° \)
Substituting the value of Angle CBE:
\( X + 130° = 180° \)
Thus,
\( X = 180° - 130° = 50° \)

Step 4: Apply Linear Pair on Angle ACF
Similarly, for angle ACF:
\( Y + \text{Angle ACF} = 180° \)
Substituting the value of Angle ACF:
\( Y + 130° = 180° \)
Thus,
\( Y = 180° - 130° = 50° \)

Step 5: Apply Angle Sum Property in Triangle ABC
The sum of angles in triangle ABC is:
\( X + Y + \text{Angle BAC} = 180° \)
Substituting the values of X and Y:
\( 50° + 50° + \text{Angle BAC} = 180° \)
This simplifies to:
\( 100° + \text{Angle BAC} = 180° \)
Thus,
\( \text{Angle BAC} = 180° - 100° = 80° \)

Step 6: Apply Linear Pair on Angle CAG
Now, we apply the linear pair on angle CAG:
\( \text{Angle BAC} + \text{Angle GAB} = 180° \)
Substituting the value of Angle BAC:
\( 80° + \text{Angle GAB} = 180° \)
Thus,
\( \text{Angle GAB} = 180° - 80° = 100° \)

Conclusion
The value of angle GAB is 100°.

---