In a triangle ABC,∠A=70∘,∠B=80∘ and D is the incentre of ΔABC.∠ACB=2× and ∠BDC=y∘. The values of x and y, respectively are.
15, 130
15, 125
35, 40
30, 150
The correct Answer is:B
To solve the problem step by step, we will analyze the triangle ABC with the given angles and find the values of x and y.
Step 1: Find Angle C
Given:
- Angle A = 70°
- Angle B = 80°
Using the property that the sum of angles in a triangle is 180°, we can find angle C:
Angle C=180°−(Angle A+Angle B)=180°−(70°+80°)=180°−150°=30°
Step 2: Determine the Incenter and Angle ACB
Since D is the incenter of triangle ABC, it bisects angle C. Therefore, angle ACB can be expressed as:
Angle ACB=2x
From Step 1, we found that angle C = 30°. Thus:
2x=30°
To find x, we divide both sides by 2:
x=30°2=15°
Step 3: Find Angle BDC
Now, we need to find angle BDC (denoted as y). In triangle BDC, we know:
- Angle DBC = 40° (since angle B = 80° and D bisects it, angle DBC = 80°/2 = 40°)
- Angle DCB = 15° (since angle ACB = 2x = 30°, and D bisects it, angle DCB = 30°/2 = 15°)
Now, we can find angle BDC using the triangle angle sum property:
Angle BDC+Angle DBC+Angle DCB=180°
Substituting the known values:
y+40°+15°=180°
Combining the angles:
y+55°=180°
Now, solving for y:
y=180°−55°=125°
Final Values
Thus, we have:
- x=15°
- y=125°
Summary
The values of x and y are:
- x=15°
- y=125°
Given:
- Angle A = 70°
- Angle B = 80°
Since D is the incenter of triangle ABC, it bisects angle C. Therefore, angle ACB can be expressed as:
Now, we need to find angle BDC (denoted as y). In triangle BDC, we know:
- Angle DBC = 40° (since angle B = 80° and D bisects it, angle DBC = 80°/2 = 40°)
- Angle DCB = 15° (since angle ACB = 2x = 30°, and D bisects it, angle DCB = 30°/2 = 15°)
Thus, we have:
- x=15°
- y=125°
The values of x and y are:
- x=15°
- y=125°
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)
35 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)
30 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)
25 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
In a triangle ABC,∠A=70∘,∠B=80∘ and D is the incentre of ΔABC,∠ACB=2x∘ and ∠BDC=y∘. The values of x and y respectively will be
A15∘,130∘B15∘,125∘C35∘,40∘D30∘,150∘In a △ABC, if 2 ∠A = 3 ∠B = 6∠C, then ∠B = ?
A30∘B90∘C60∘D45∘I is the incentre of a triangle ABC. If ∠ABC=65∘ and ∠ACB=55∘, then the value of ∠BICis
A130∘B120∘C140∘D110∘
In a triangle ABC,
12∠A+13∠C+12∠B= 80° then what is
∠C equal to ?
View SolutionIn a triangle ABC,∠A=600andb:e=(√3+1):2, then find the value of (∠B−∠C).
View SolutionIn a ΔABC,∠A+∠B=70∘ and ∠B+∠C=130∘, value of ∠A is
View SolutionFind the value of x and y respectively, if ΔABC≅ΔQRP.
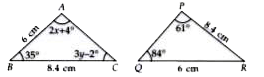
View SolutionIn the given figure, ∠A=80∘,∠B=60∘,∠C=2x∘and∠BDC=y∘. BD and CD bisect angles B and C respectively.

The values of x and y respectively are :
View Solution
