In a triangle ABC, ∠A=70∘,∠B=80∘ and D is the incentre of ΔABC.∠ACB=2X∘ and ∠BDC=y∘. The values of x and y, respectively are
15, 130
15, 125
35, 40
30, 150
To solve the problem step by step, we will follow the reasoning outlined in the video transcript.
Step 1: Find Angle C
Given:
- Angle A = 70°
- Angle B = 80°
We know that the sum of angles in a triangle is 180°. Therefore, we can find Angle C as follows:
Angle C=180°−Angle A−Angle B
Substituting the values:
Angle C=180°−70°−80°=180°−150°=30°
Step 2: Relate Angle C to X
According to the problem, Angle ACB (which is Angle C) is given as:
Angle ACB=2X
Since we found Angle C to be 30°, we can set up the equation:
2X=30°
Now, solving for X:
X=30°2=15°
Step 3: Find Angle BDC (Y)
D is the incenter of triangle ABC. The angle BDC can be calculated using the formula:
Angle BDC=90°+12×Angle A
Substituting the value of Angle A:
Angle BDC=90°+12×70°
Calculating:
Angle BDC=90°+35°=125°
Thus, we have:
Y=125°
Final Values
The values of X and Y are:
- X=15°
- Y=125°
Summary
The final answer is:
- X=15°
- Y=125°
Given:
- Angle A = 70°
- Angle B = 80°
According to the problem, Angle ACB (which is Angle C) is given as:
D is the incenter of triangle ABC. The angle BDC can be calculated using the formula:
The values of X and Y are:
- X=15°
- Y=125°
The final answer is:
- X=15°
- Y=125°
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a triangle ABC,∠A=70∘,∠B=80∘ and D is the incentre of ΔABC,∠ACB=2x∘ and ∠BDC=y∘. The values of x and y respectively will be
A15∘,130∘B15∘,125∘C35∘,40∘D30∘,150∘ - Question 2 - Select One
In a triangle ABC,∠A=70∘,∠B=80∘ and D is the incentre of ΔABC.∠ACB=2× and ∠BDC=y∘. The values of x and y, respectively are.
A15, 130B15, 125C35, 40D30, 150 - Question 3 - Select One
I is the incentre of the triangle ABC. If ∠ABC=60∘ and ∠ACB=50∘ then ∠BIC is
A55∘B125∘C70∘D65∘
In ΔABC if AB=ACand∠B=70∘, then ∠C=2a∘. Find the value of a
View SolutionIn a ΔABC,∠A=2∠B=3∠C, find each of the triangle.
View SolutionIn a triangle ABC, if 2 ∠A=3∠B=6∠C, then what is ∠A+∠C equal to ?
View SolutionFind the value of x and y respectively, if ΔABC≅ΔQRP.
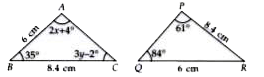 View Solution
View SolutionIn a parallelogram ABCD if ∠A=(3x−20)∘,∠B=(y+15)∘and∠C=(x+40)∘, then the values of x and y respectgively are
View Solution

