Question

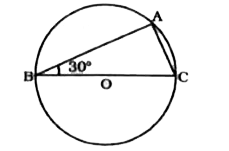
ABCD is a quadrilateral inscribed in a circle with centre O. If $\angle COD={120}^{\circ }$ and $\angle BAC={30}^{\circ }$, then $\angle BCD$ is :

Options

A. `75^@`
B. `90^@`
C. `120^@`
D. `60^@`

Answer

B

Explanation

To solve the problem, we need to find the angle $$\angle BCD$$ in the cyclic quadrilateral $$ABCD$$ inscribed in a circle. We are given the following information:

- $$\angle COD={120}^{\circ }$$
- $$\angle BAC={30}^{\circ }$$

1. Understanding the Angles:
- Since \( ABCD \) is a cyclic quadrilateral, the angles at the center of the circle and the angles at the circumference are related. The angle at the center \( \angle COD \) is twice the angle at the circumference \( \angle CAD \) (which is the same as \( \angle BAC \)).

2. Finding \( \angle CAD \):
- We know that \( \angle COD = 120^\circ \). Therefore, the angle at the circumference \( \angle CAD \) can be calculated as:
\( \angle CAD = \frac{1}{2} \times \angle COD = \frac{1}{2} \times 120^\circ = 60^\circ \)

3. Finding \( \angle BAD \):
- We are also given \( \angle BAC = 30^\circ \). Thus, we can find \( \angle BAD \) as:
\( \angle BAD = \angle BAC = 30^\circ \)

4. Finding \( \angle BOD \):
- The angle \( \angle BAD \) and \( \angle CAD \) together form the angle \( \angle BOD \):
\( \angle BOD = \angle BAD + \angle CAD = 30^\circ + 60^\circ = 90^\circ \)

5. Using the Cyclic Quadrilateral Property:
- In a cyclic quadrilateral, the sum of the opposite angles is \( 180^\circ \). Therefore, we can use this property to find \( \angle BCD \):
\( \angle BCD + \angle BAD = 180^\circ \)
- Substituting the value of \( \angle BAD \):
\( \angle BCD + 90^\circ = 180^\circ \)
- Solving for \( \angle BCD \):
\( \angle BCD = 180^\circ - 90^\circ = 90^\circ \)

Conclusion:
Thus, the angle \( \angle BCD \) is \( 90^\circ \).