The internal bisectors of ∠ABCand∠ACBof ΔABCmeet each other at O. If ∠BOC=110∘, then ∠BAC is equal to
40∘
55∘
90∘
110∘
The correct Answer is:A
To solve the problem, we need to find the measure of angle ∠BAC given that the internal bisectors of angles ∠ABC and ∠ACB meet at point O and that ∠BOC=110∘.
1. Understanding the Relationship:
The internal angle bisectors of angles ∠ABC and ∠ACB intersect at point O. The angle formed at point O between these two bisectors is ∠BOC.
2. Using the Angle Bisector Theorem:
We know from geometry that the angle formed at the intersection of the angle bisectors can be expressed as:
∠BOC=90∘+12∠BAC
3. Substituting the Given Value:
We are given that ∠BOC=110∘. We can substitute this value into the equation:
110∘=90∘+12∠BAC
4. Isolating ∠BAC:
To find ∠BAC, we first subtract 90∘ from both sides of the equation:
110∘−90∘=12∠BAC
This simplifies to:
20∘=12∠BAC
5. Solving for ∠BAC:
Now, we multiply both sides by 2 to solve for ∠BAC:
∠BAC=2×20∘=40∘
Final Answer:
Thus, the measure of ∠BAC is 40∘.
---
The internal angle bisectors of angles ∠ABC and ∠ACB intersect at point O. The angle formed at point O between these two bisectors is ∠BOC.
We know from geometry that the angle formed at the intersection of the angle bisectors can be expressed as:
∠BOC=90∘+12∠BAC
We are given that ∠BOC=110∘. We can substitute this value into the equation:
110∘=90∘+12∠BAC
To find ∠BAC, we first subtract 90∘ from both sides of the equation:
110∘−90∘=12∠BAC
This simplifies to:
20∘=12∠BAC
Now, we multiply both sides by 2 to solve for ∠BAC:
∠BAC=2×20∘=40∘
Thus, the measure of ∠BAC is 40∘.
Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF
25 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
70 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
Internal bisectors of angles ∠Band∠C of a triangle ABC meet at O. If ∠BAC=80∘, then the value of ∠BOC is
A120∘B140∘C110∘D130∘The internal bisectors of ∠Band∠C of ΔABC meet at O. If ∠A=80∘ then ∠BOC is :
A50∘B160∘C100∘D130∘CF is the internal bisector of angle C of ΔABC then CF is equal to
A2aba+bcosC2Ba+b2abcosC2CbsinAsin(B+C2)Dnone of these
The internal bisectors of the angles B and C of a triangle ABC meet at I. If ∠BIC=∠A2+X then X is equal to
View SolutionO is the orthocentre of ΔABC, and if ∠BOC=110∘, then ∠BAC will be
View SolutionIn the figure ΔABCis inscribed in a circle with centre O. If ∠ABC=30∘ then ∠ACBis equal to
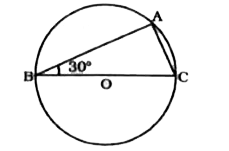
View SolutionCF is the internal bisector of angle C of ∠ABC, then CF is equal to
View SolutionIn a ΔABC, the internal angle bisector of ∠ABC and ∠ACB meets at point ‘O’. If the ∠BOC is 134∘, then find ∠BAC.
View Solution
