Circum-centre of ΔPQR is O. If ∠QPR=55∘ and ∠QRP=75∘, what is the value (in degrees) of ∠OPR?
45
40
65
70
The correct Answer is:B
To find the value of angle ∠OPR in triangle PQR with circumcenter O, we can follow these steps:
Step 1: Identify the given angles
We know:
- ∠QPR=55∘
- ∠QRP=75∘
Step 2: Calculate the third angle ∠PQR
Using the angle sum property of triangles, which states that the sum of the angles in a triangle is 180∘:
∠PQR=180∘−∠QPR−∠QRP
Substituting the known values:
∠PQR=180∘−55∘−75∘
∠PQR=180∘−130∘=50∘
Step 3: Understanding the angles at the circumcenter
In triangle POR, where O is the circumcenter, the angle ∠POR at the center is twice the angle ∠PQR at the circumference:
∠POR=2×∠PQR=2×50∘=100∘
Step 4: Set up the equation for triangle POR
In triangle POR, we have:
- ∠OPR=x
- ∠ORP=x
- ∠POR=100∘
Using the angle sum property again:
∠OPR+∠ORP+∠POR=180∘
Substituting the known values:
x+x+100∘=180∘
2x+100∘=180∘
Step 5: Solve for x
Subtract 100∘ from both sides:
2x=180∘−100∘
2x=80∘
Now, divide by 2:
x=40∘
Conclusion
Thus, the value of ∠OPR is 40∘.
---
We know:
- ∠QPR=55∘
- ∠QRP=75∘
Using the angle sum property of triangles, which states that the sum of the angles in a triangle is 180∘:
∠PQR=180∘−∠QPR−∠QRP
Substituting the known values:
∠PQR=180∘−55∘−75∘
∠PQR=180∘−130∘=50∘
In triangle POR, where O is the circumcenter, the angle ∠POR at the center is twice the angle ∠PQR at the circumference:
∠POR=2×∠PQR=2×50∘=100∘
In triangle POR, we have:
- ∠OPR=x
- ∠ORP=x
- ∠POR=100∘
∠OPR+∠ORP+∠POR=180∘
Substituting the known values:
x+x+100∘=180∘
2x+100∘=180∘
Subtract 100∘ from both sides:
2x=180∘−100∘
2x=80∘
Now, divide by 2:
x=40∘
Thus, the value of ∠OPR is 40∘.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - TRY YOURSELF25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)70videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
Circum-centre of ΔPQR is O. If ∠QPR=55∘ and ∠QRP=75∘, what is the value (in degrees) of ∠OPR?
A45B40C65D70 - Question 2 - Select One
In the given figure, O is the centre of the circle, ∠PQR=100∘ and ∠STR=105∘. What is the value (in degrees) of ∠OSP?
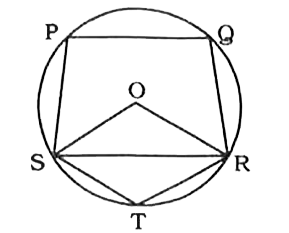 A(a) 95B(b) 45C(c) 75D(d) 65
A(a) 95B(b) 45C(c) 75D(d) 65 - Question 3 - Select One
In the given figure, O is the centre of the circle, ∠CAO = 35∘ and ∠CBO= 45∘. What is the value (In degrees) of ∠AOB?
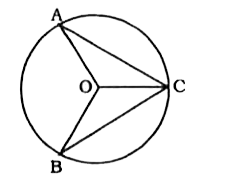 A150B110C160D130
A150B110C160D130
Triangle PQR is inscribed in a circle such that P Q and R lie on the circumference. If PQ is the diameter of the circle and ∠PQR=40∘, then what is the value (in degree) of QPR?
View SolutionIn the given figure. 0 is centre of the circle. Circle has 3 tangents. If QPR = 45∘, then what is the value (in degrees) of ∠QOR?
 View Solution
View SolutionIn the given figure, O is the centre of the circle, ∠CAO = 35∘ and ∠CBO= 45∘. What is the value (In degrees) of ∠AOB?
 View Solution
View SolutionIn ΔPQR,SandT are the mid points of sides PQ and PR respectively. If ∠QPR=45∘and∠PRQ=55∘, then what is the value (in degrees) of ∠QST ?
View SolutionIn triangle PQR, the internal bisector of ∠Q and ∠R meets at 0. If ∠QPR=70∘, then what is the value (in degrees) of ∠QOR?
View Solution

