Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px+qy, where p,q>0. Condition on p and q so that the minimum of Z occurs at (3,0) and (1, 1) is : Solution in Punjabi
p=2q
p=q2
p=3q
p=q
The correct Answer is:B
Step by step video, text & image solution for Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px+qy, where p, qgt 0. Condition on p and q so that the minimum of Z occurs at (3,0) and (1, 1) is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-II : FILL IN THE BLANKS QUESTIONS)
11 Videos
- LINEAR PROGRAMMING BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-III : TRUE OR FALSE QUESTIONS)
10 Videos
- LINEAR PROGRAMMING BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 6 MARKS
7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ACCURATE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS CARRYING 4 MARKS
27 Videos
- MATRICESBOOK - ACCURATE PUBLICATIONCHAPTER - MATRICESEXERCISE - QUESTIONS CARRYING 6 MARKS
4 Videos
Similar Questions
In a LPP, the linear inequalities or restrictions on the variables are called ..............
View SolutionIf the feasible region for a linear programming problem is bounded, then the objective function Z = ax+by has both a maximum and a minimum value on R.
View SolutionFind the maximum value of f = x+2 y subject to the constraints
2x+3y≤6
x+4y≤4
x,y≥0
View SolutionWrite the value of tan−1[2sin(2cos−1√32)].
View SolutionIf A=⎡⎢⎣1−202130−21⎤⎥⎦,B=⎡⎢⎣72−6−21−3−425⎤⎥⎦ , find AB Also solve x−2y=10,2x+y+3z=8,−2y+z=7
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
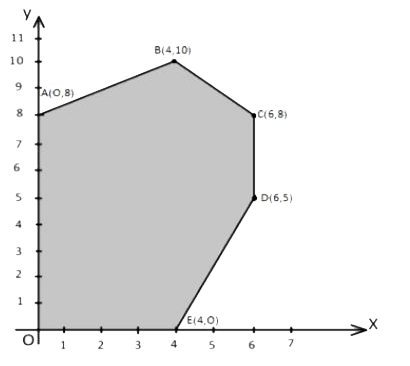
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.
View Solutionकिसी राखक व्यवरोधों के निकाय द्वारा निधारित एक सुसंगत क्षत्र क काणाय बिन्दु (0, 3), (1,1) तथा (3, 0) हा मान लीजिए कि Z = px + qy, (जहाँ p,q>0) उद्देश्य फलन है। p तथा q पर लगने वाला वह प्रतिबन्ध, जिससे Z का न्यूनतम मान (3, 0) तथा (1,1) पर प्राप्त होगा।
View SolutionThe vertices of the feasible region determined by some linear constraints are (0,2),(1,1),(3,3),(1,5). Let Z=px+qy where p,q>0. The condition on pandq so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is .......
View SolutionThe corner points of the feasible region determined by some inequality are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p,q>0 condition on p and q so that the maximum of Z occurs at both (15, 15) and (0, 20) is …………
View SolutionThe vertices of the feasible region determined by some linear constraints are (0, 2), (1, 1), (3, 3), (1, 5). Let Z = px + qy where p, q gt 0. The condition on p and q so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is ……..
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0,10) , (5,5) (25,20),(0,30) Let z = px + qy , where p,q>0 Condition on p and q so that te maximum of z occurs at both the points (25,20 ) and (0,30) is ………
View SolutionThe occurs point of the feasible region for an L.P.P. are (0, 3), (1, 1) and (3, 0). If objective function is Z=px+qy,p,q>0, then the condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
View SolutionThe corner points of the feasible region determined by the system linear constraints are (0,10), (5,5), (15,15), (0,20). Let Z = px+ qy, where p, q>0, condition on p and q so that the maximum of Z occurs at both the points (15,15) and (0,20) is
View Solution
