The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0,40), (20,40), (60, 20), (60, 20), (60,0). The objective function is Z=4x+3 y Compare the quantity in Column A and Column B
Column AColumn BMaximum of Z325 Solution in Punjabi
The quantity in column A is greater
The quantity in column B is greater
The two quantities are equal
The relationship can not be determined on the basis of the information supplied
The correct Answer is:B
Step by step video, text & image solution for The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0,40), (20,40), (60, 20), (60, 20), (60,0). The objective function is Z=4x+3 y Compare the quantity in Column A and Column B {:("Column A","Column B"),("Maximum of Z",325):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-II : FILL IN THE BLANKS QUESTIONS)
11 Videos
- LINEAR PROGRAMMING BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 1 MARK (TYPE-III : TRUE OR FALSE QUESTIONS)
10 Videos
- LINEAR PROGRAMMING BOOK - ACCURATE PUBLICATIONCHAPTER - LINEAR PROGRAMMING EXERCISE - QUESTIONS CARRYING 6 MARKS
7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ACCURATE PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS CARRYING 4 MARKS
27 Videos
- MATRICESBOOK - ACCURATE PUBLICATIONCHAPTER - MATRICESEXERCISE - QUESTIONS CARRYING 6 MARKS
4 Videos
Similar Questions
In a LPP, the linear inequalities or restrictions on the variables are called ..............
View SolutionIf the feasible region for a linear programming problem is bounded, then the objective function Z = ax+by has both a maximum and a minimum value on R.
View SolutionFind the maximum value of f = x+2 y subject to the constraints
2x+3y≤6
x+4y≤4
x,y≥0
View SolutionWrite the value of tan−1[2sin(2cos−1√32)].
View SolutionIf A=⎡⎢⎣1−202130−21⎤⎥⎦,B=⎡⎢⎣72−6−21−3−425⎤⎥⎦ , find AB Also solve x−2y=10,2x+y+3z=8,−2y+z=7
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
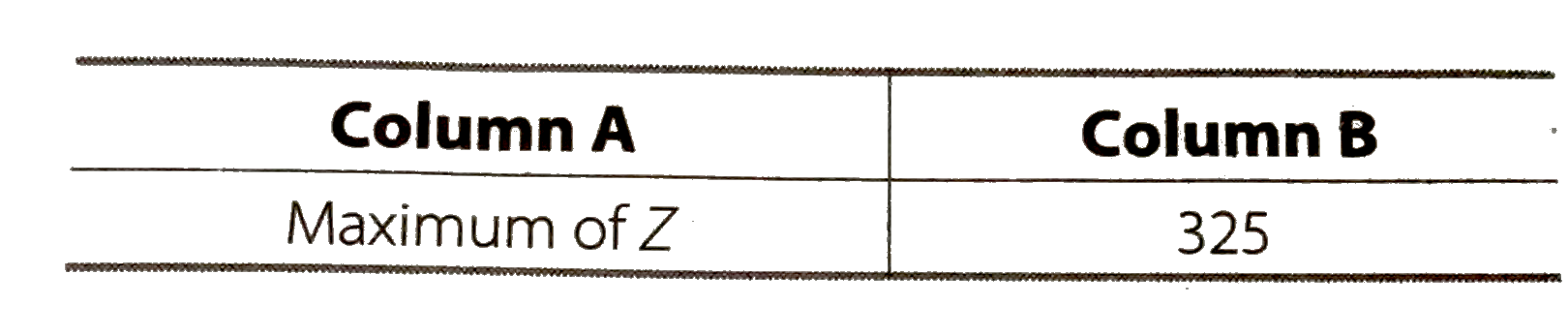
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View SolutionColumn Ax=a,y=2b,z=3c,x:y:z=1:2:3Column Bx+y+za+b+c2
View SolutionLet A(0, 75), B(90, 0) , C(60, 40) and D(45, 25) be the corner points of the bounded feasible region of a LPP . If the objective function is Z=3x+4y, then Z is maximum at corner point-
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
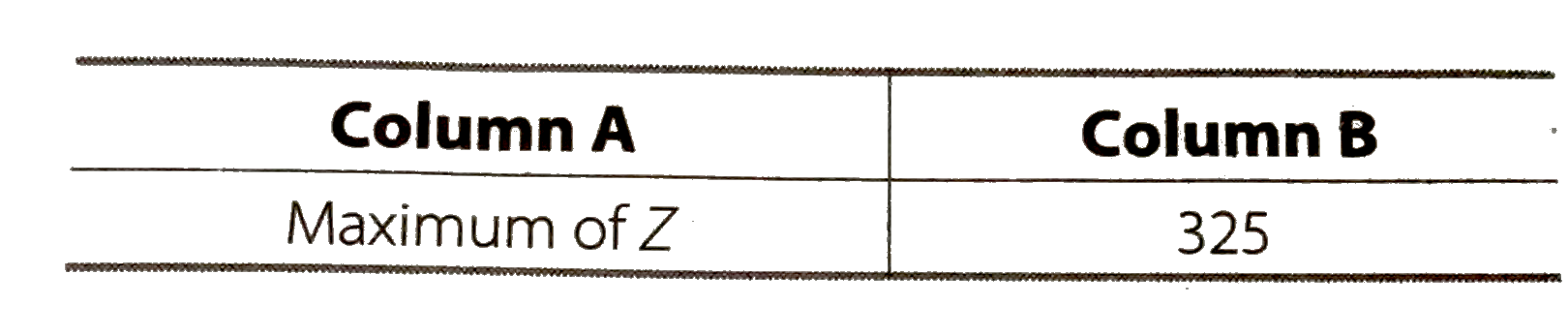
View Solutionव्यवरोधों के एक निकाय द्वारा निर्धारित किसी सुसंगत क्षेत्र के कोनीय बिंदु (0, 0), (0, 40), (20, 40), (60, 20), (60, 0) हैं। उद्देश्य फलन Z = 4x + 3y है। 26. स्तंभ A तथा स्तंभ B की राशियों की तुलना कीजिए।

View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is z = 4x + 3y.
Compare the quantity in Column A and Column B

View Solutionz = 30x - 30y + 1800 is a objective function. The corner points of the feasible region are (15, 0), (15, 15), (10, 20), (0, 20) and (0, 15). z has the minimum value at …….. point.
View SolutionThe corner points of the bounded feasible region are (60, 0), (120, 0), (60, 40), (40, 20) and (20, 30). For the objective function z = 5x + 10y ………
(i) Maximum value of z.
(ii) Minimum value of z.
(iii) Maximum value of z has at ………..
(iv) Minimum value of z has at ...........
View SolutionThe corner points of the feasible region are (0, 0), (16, 0), (8, 12), (0, 20). The maximum value of the objective function Z = 22x + 18y is …………
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View Solution
