The instantaneous angular position of a point on a rotating wheel is given by the equation θ(t)=2t3−6t2. The torque on the wheel becomes zero at:Solution in Tamil
t=2s
t=1s
t=0.2s
t=0.25s
Step by step video & image solution for The instantaneous angular position of a point on a rotating wheel is given by the equation theta (t)=2t^3-6t^2. The torque on the wheel becomes zero at: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Assuming the sun to have a spherical outer surface of radiating like a black body at temperature t∘C, the power received by a unit surface,(normal to the incident rays) at a distance R from the centre of the sun is
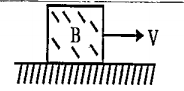
01:44View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction betweenB and the surface , block B will come to rest after a time.
 .01:35View Solution
.01:35View SolutionA constant torque is acting on a wheel. If starting from rest, the wheel makes n rotations in t seconds, show that the angular
acceleration is given by α=4πnt2rads−2.03:29View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation theta(t) = 2t^(3) - 6 t^(2) The torque on the wheel becomes zero at
01:25View SolutionA wheel rotates around a stationary axis so that the rotation angle theta varies with time as theta=2t^(2) radian. Find the total acceleration of the point A at the rim at the moment t=0.5 s If the radius of wheel is 1 m .
03:52View SolutionThe angular displacement at any time t is given by theta(t) = 2t^(3)-6^(2) . The torque on the wheel will be zero at
03:19View SolutionA constant torque is acting on a wheel. If starting from rest, the wheel makes n rotations in t seconds, Show that the angular acceleration is given by alpha = \frac { 4 \pi n } { t ^ { 2 } } rad s^-2 .
03:06View SolutionThe angular displacement θ radians of a fly wheel varies with time t seconds and follow the equation θ=9t2−2t3. Determine the angular velocity and acceleration of the fly wheel when time t =1 seconds and (ii) The time when the angular acceleration is zero.
03:41View Solutionएक घूर्णन करते पहिए पर एक तात्कालिक बिंदु की स्थिति θ(t)=2t3−6t2 समीकरण से दी गई है | कितने समय पश्चात पहिए का बल - आघूर्ण शून्य होगा ?
02:40View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation theta (t) = 2t^3 - 6t^2 . The torque on the wheel becomes zero at : .......... .
02:08View Solutionवृत्ताकार पथ में घूर्णन करते हुए किसी पहिये पर स्थित बिन्दु की ताक्षणिक कोणीय स्थिति समीकरण θ(t)=2t3−12t2 से निरूपित की जाती है, तो पहिये पर लगने वाले बल आघूर्ण का मान शून्य होगा
View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation θ(t)=2t3−6t2. The torque on the wheel becomes zero at ………. s
03:42View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation theta (t) = 2t^(3) - 6t^(2) . The torque on the wheel becomes zero at
02:49View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation
θ(t)=2t3−6t2
The torque on the wheel becomes zero at a) t = 1 s b) t = 0.5 s c) t = 0.25 s d) t = 2 s02:00View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation theta = 2t^3 - 6t^2 . After what time the torque on the wheel be zeron?
01:59View SolutionThe instantaneous angular position of a point on a rotating wheel is given by the equation
θ(t)=2t3−6t2
The torque on the wheel becomes zero at03:06View Solution

