The coefficient of correlation between random variables X and Y is 0.28, covariance between X and Y is 7.6 and the variance of X is 9, then the standard deviation of Y series is
9.8
10.1
9.05
10.05
The correct Answer is:C
To find the standard deviation of the Y series given the correlation coefficient, covariance, and variance of X, we can use the formula for the correlation coefficient (r):
1. Understand the formula for the correlation coefficient (r):
r=Cov(X,Y)σX⋅σY
where:
- r is the coefficient of correlation,
- Cov(X,Y) is the covariance between X and Y,
- σX is the standard deviation of X,
- σY is the standard deviation of Y.
2. Identify the given values:
- Coefficient of correlation, r=0.28
- Covariance, Cov(X,Y)=7.6
- Variance of X, Var(X)=9
3. Calculate the standard deviation of X:
σX=√Var(X)=√9=3
4. Rearrange the correlation formula to solve for σY:
σY=Cov(X,Y)r⋅σX
5. Substitute the known values into the rearranged formula:
σY=7.60.28⋅3
6. Calculate the denominator:
0.28⋅3=0.84
7. Now calculate σY:
σY=7.60.84≈9.05
Final Answer:
The standard deviation of the Y series is approximately 9.05.
---
r=Cov(X,Y)σX⋅σY
where:
- r is the coefficient of correlation,
- Cov(X,Y) is the covariance between X and Y,
- σX is the standard deviation of X,
- σY is the standard deviation of Y.
- Coefficient of correlation, r=0.28
- Covariance, Cov(X,Y)=7.6
- Variance of X, Var(X)=9
σX=√Var(X)=√9=3
σY=Cov(X,Y)r⋅σX
σY=7.60.28⋅3
0.28⋅3=0.84
σY=7.60.84≈9.05
The standard deviation of the Y series is approximately 9.05.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - PROBLEM SET (1) TRUE/FALSE6videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - PROBLEM SET (1) (FILL IN THE BLANKS)10videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - QUESTION (STATE GIVING REASONS, WHETHER EACH OF THE FOLLOWING STATEMENTS IS TRUE OR FALSE)10videos
CORRELATION AND REGRESSION
- BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test13videos
CONCEPTS OF SET THEORY
- BOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)1videos
DEFINITE INTEGRAL
Similar Questions
Knowledge Check
- Question 1 - Select One
If the coefficient of correlation between x and y os 0.6, covariance is 27 and variance of y is 25, then what is the variance x?
A9/5B81/25C9D81 - Question 2 - Select One
Question Stimulus :-
If coefficient of correlation between the variables x and y is zero, thenAx and y have no relationBy decreases as x increasesCy increases as x increasesDNone of these - Question 3 - Select One
Correlation coefficient r of two variables X and Y is positive when
AσX+Y>σX−YBσX−Y>σX+YCσX+Y=0Dnone of these
Calculate the coeficient of correlation between X and Y.
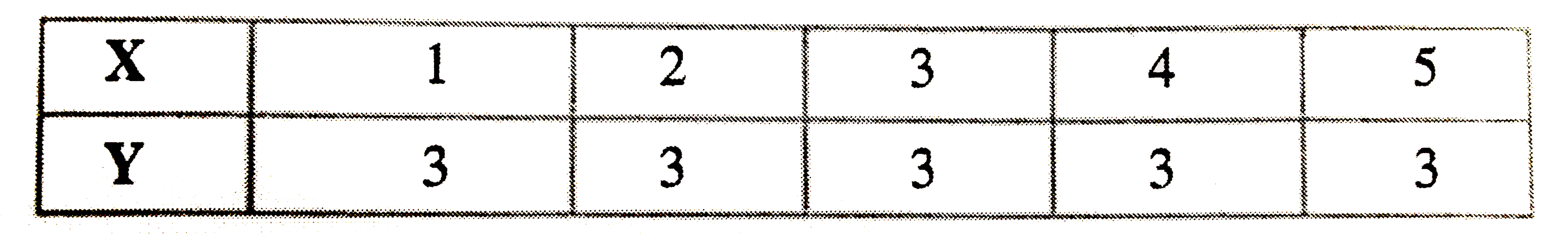 View Solution
View SolutionFind out coefficient of rank correlation between X and Y
 View Solution
View SolutionThe co-efficient of correlation between two variables x and y is 0.5. Their co-variance is 15 and σx=6, Then σy=
View SolutionThe coefficient of correlation between X and Y is 0.6. Their covariance is 4.8 var (x)=9. Find the value of σy.
View SolutionIf the correlation coefficient between x and y is 0.6, covariance is 27 and variance of y is 25, then what is the variance of x?
View Solution


