A butterfly is flying with a velocity 4√2m/s in North-East direction. Wind is slowly blowing at 1 m/s from North to South. The resultant displacement of the butterfly in 3 seconds is :
3 m
20 m
12√2m
15 m
To solve the problem, we need to find the resultant displacement of the butterfly after 3 seconds, taking into account its velocity and the effect of the wind.
1. Identify the Velocity of the Butterfly:
The butterfly is flying at a velocity of 4√2m/s in the North-East direction. In vector form, this can be expressed as:
→Vb=4√2m/s⋅(cos45∘^i+sin45∘^j)
Since cos45∘=sin45∘=1√2, we can simplify this to:
→Vb=4√2⋅(1√2^i+1√2^j)=4^i+4^j
2. Identify the Velocity of the Wind:
The wind is blowing from North to South at 1m/s. In vector form, this can be expressed as:
→Vw=−1^j
3. Calculate the Resultant Velocity:
The resultant velocity of the butterfly with respect to the ground is the sum of its velocity and the wind's velocity:
→Vr=→Vb+→Vw=(4^i+4^j)+(0^i−1^j)=4^i+(4−1)^j=4^i+3^j
4. Calculate the Magnitude of the Resultant Velocity:
The magnitude of the resultant velocity can be calculated using the Pythagorean theorem:
|→Vr|=√(4)2+(3)2=√16+9=√25=5m/s
5. Calculate the Displacement in 3 Seconds:
Displacement is given by the formula:
Displacement=Velocity×Time
Substituting the values we have:
Displacement=5m/s×3s=15m
Thus, the resultant displacement of the butterfly in 3 seconds is 15 meters.
The butterfly is flying at a velocity of 4√2m/s in the North-East direction. In vector form, this can be expressed as:
→Vb=4√2m/s⋅(cos45∘^i+sin45∘^j)
Since cos45∘=sin45∘=1√2, we can simplify this to:
→Vb=4√2⋅(1√2^i+1√2^j)=4^i+4^j
The wind is blowing from North to South at 1m/s. In vector form, this can be expressed as:
→Vw=−1^j
The resultant velocity of the butterfly with respect to the ground is the sum of its velocity and the wind's velocity:
→Vr=→Vb+→Vw=(4^i+4^j)+(0^i−1^j)=4^i+(4−1)^j=4^i+3^j
The magnitude of the resultant velocity can be calculated using the Pythagorean theorem:
|→Vr|=√(4)2+(3)2=√16+9=√25=5m/s
Displacement is given by the formula:
Displacement=Velocity×Time
Substituting the values we have:
Displacement=5m/s×3s=15m
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION-B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)
40 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
An aeroplane takes off from Mumbai to Delhi with velocity 50 kph in north-east direction. Wind is blowing at 25 kph from north to south. What is the resultant displacement of aeroplane in 2 hrs.
View SolutionAn aeroplane takes off from Mumbai to Delhi with velocity 50 kph at an angle 30∘ north of east. Wind is blowing at 25 kph from north to south. What is the resultant displacement of aeroplane in 2 hrs. (in km)
View Solution
Knowledge Check
The velocity of a body at time t=0 is 10√2m/s in the north-east direction and it is moving with an acceleration of 2m/s directed towards the south. The magnitude and direction of the velocity of the body after 5 sec will be
A10m/s, towards eastB10m/s,towards northC10m/s, towards southD10m/s, towards north-eastA 400 m wide river is flowing from west to east at velocity 3m/s. A boat starts from one bank and it crosses the river along the shortest path. When it reaches the middle of river, wind starts blowing horizontally along north-east at a velocity √2 m/s . Due to this, the direction of rowing of boat has to be changed for the boat to move along the shortest path. If the velocity of boat in still water with no wind blowing is 5 m/s, then choose the correct option(s).
AThe initial direction of rowing of boat is at an angle of53∘ with upstream directionBTime taken to reach the middle of river is 50 secondsCAfter the wind starts blowing, the direction of rowing of boat is 37∘ with upstream directionDTotal time taken by the boat to cross the river along the shortest path is 100 secondsA motor car A is travelling with a velocity of 20m/s in the north-west direction and another motor car B is travelling with a velocity of 15m/s in the north-east directions.The magnitude of relative velocity of B with respect to A is.
A25m/sB15m/sC20m/sD35m/s
Bird is flying in north-east direction with v=4√2ms with respect to the wind and the wind is blowing from north to south with speed 1 m/s. Find the magnitude of the displacement of bird in 3 sec.
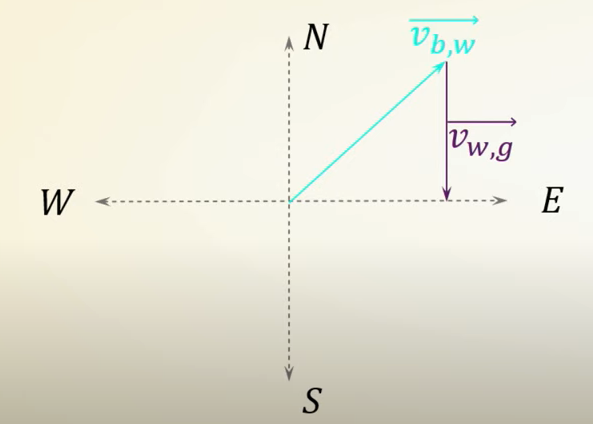
View Solution47.A man moves 10m in a direction of 37^(@) East of North then 5sqrt(2)m in South-East direction and finally 20m in a direction of 53^(@) South of West.Find the magnitude of resultant displacement of man?
View SolutionA butterfly is flying with velocity 10ˆi+12ˆjm/s and wind is blowing along x axis with velocity u . If butterfly starts motion from A and after some time reaches point B, find the value of u.
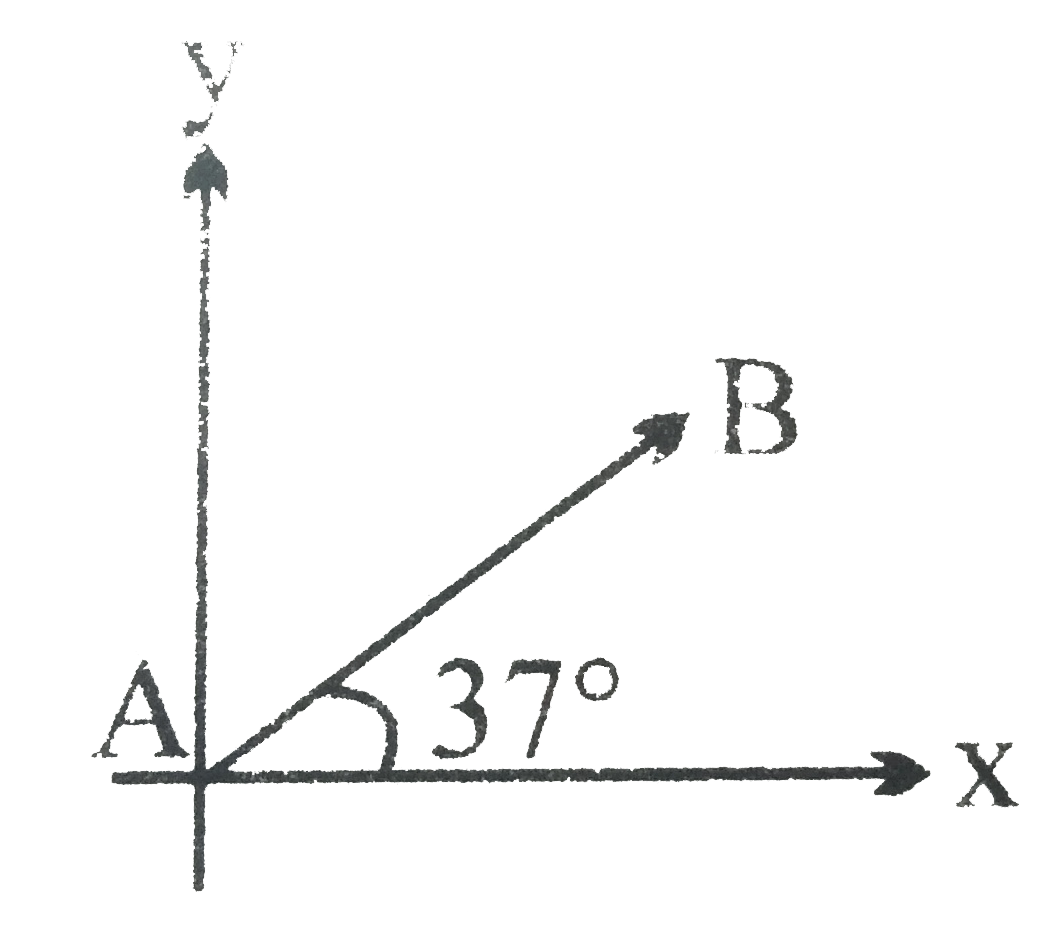
View SolutionAs insect moves 3cm towards north,4m towards east and then 5m vertically up Then its resultant displacement is
View SolutionA hydrogen is flying eastward with speed 12ms−1 , when wind starts blowing from north to south with speed 5ms−1 what is the resultant velocity of balloon ?
View Solution
