In figure ∠ABD=∠ACD,AD is bisectyor of ∠BACandAD meets BC at D. Prove that D is mid-point of BC.
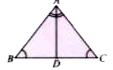
Step by step video & image solution for In figure angleABD=angleACD, AD is bisectyor of angleBAC and AD meets BC at D. Prove that D is mid-point of BC. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, if ∠BAC=90∘ and AD⊥BC, then:
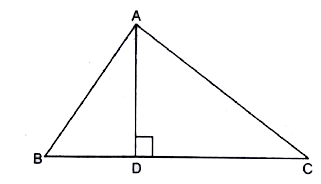 ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
AB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionInΔABC,AD is the bisector of∠A meeting BC at D, CF⊥AB and E is the mid-point of AC. Then median of the triangle is
View SolutionIn ΔABC,∠C is obtuse. The exteral bisector of ∠Aand∠B meet the extended line BC and AC at point D and E. If AB = AD = BE then find ∠ACD?
View SolutionIn the given figure BX is the angle bisector of ∠ABC,E is mid point of ADandD is the mid point of BC then BEEX is [Diagram not to scale]
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
View SolutionIn the adjoining figure, in ΔABC, point D is on side BC such that, ∠BAC=∠ADC. Prove that, CA2=CB×CD.
View SolutionIn △ABC,AB>AC and D is any point on BC. Prove that, AB > AD.
View Solution
