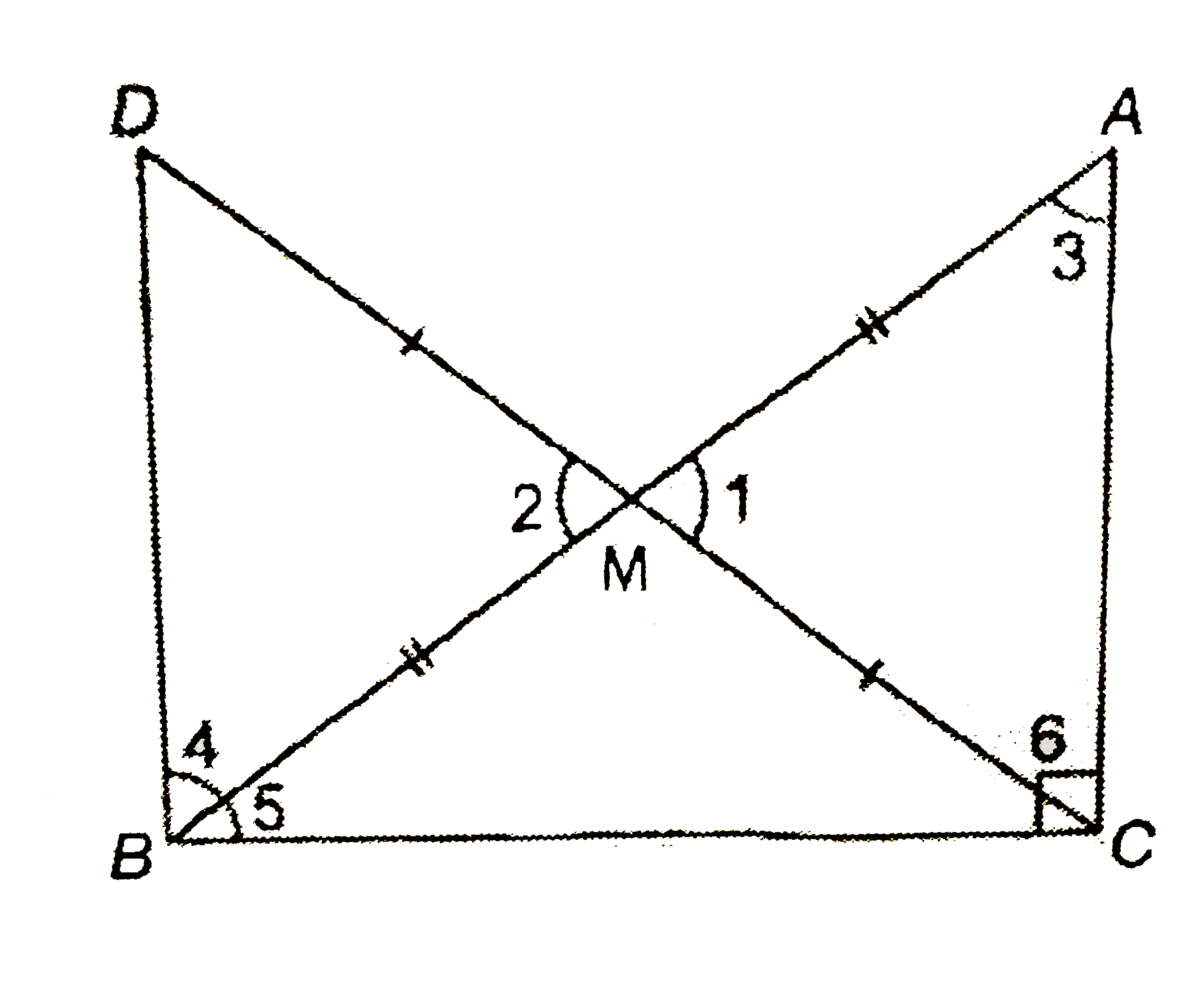
In right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that

∠DBC is right angle.
Step by step video & image solution for In right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that angleDBC is right angle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.2)
Explore 9 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.3)
Explore 10 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:SOLVED EXAMPLES
Explore 14 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
In right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that

ΔAMC≅ΔBMD
View SolutionIn right triangle ABC, right angled at C, Mis the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that

ΔDBC≅ΔACB
View Solution
Knowledge Check
In right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that
(i) ΔAMC≅ΔBMD (ii) ∠DBC=∠ACB
(iii) ΔDBC≅ΔACB (iv) CM=12AB
 AASABRHSCSSSDSAS
AASABRHSCSSSDSASABC is right angled triangle, right angled at C . D is the midpoint of BC. Then , tanθtanϕ =
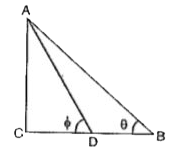 A1B1√2C12D2
A1B1√2C12D2
In right triangle ABC, right-angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig. 7.23). Show that:
(i) ΔAMC≅ΔBMD
(ii) ∠DBC is a right angle
(iii) ΔDBC≅ΔACB
(iv) CM=12AB
View SolutionIn right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that
(i) ΔAMC≅ΔBMD (ii) ∠DBC=∠ACB
(iii) ΔDBC≅ΔACB (iv) CM=12AB

View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=90∘ (iii)DBC≅ACB (iv) CM=12AB
View SolutionIn right angled triangle ABC, right angled at C, show that tanA+tanB=c2ab.
View SolutionIn a right triangle ABC , right angled at C , if ∠B=60o and AB=15 units. Find the remaining angles and sides.
View SolutionIn a right ABC right-angled at C , if D is the mid-point of BC , prove that BC2=4 (AD2−AC2) .
View Solution