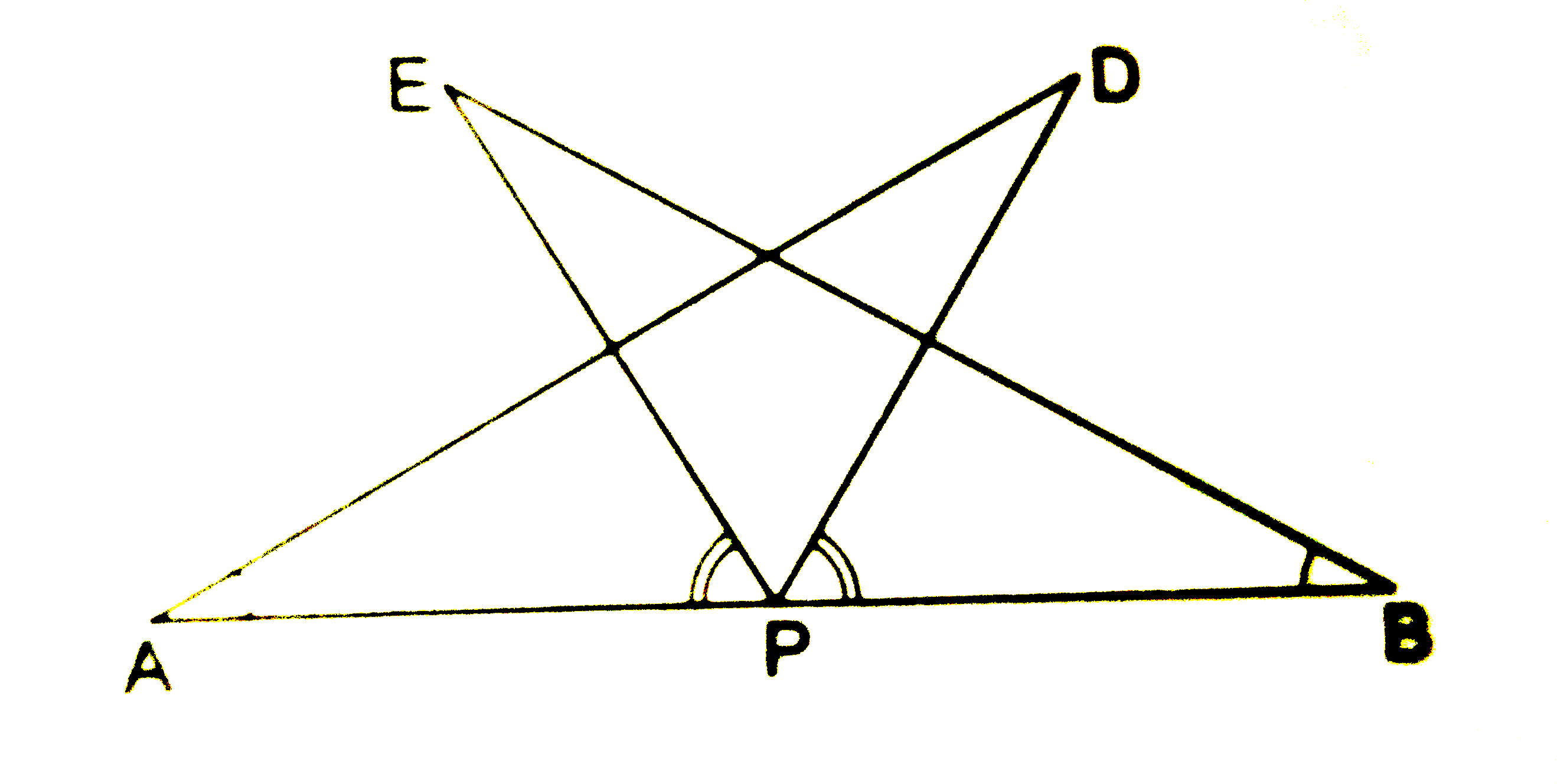
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

AD=BE
Step by step video & image solution for AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that angleBAD = angleABE and angleEPA = angleDPB (see figure). Show that AD=BE by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.2)
Explore 9 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:NCERT SECTION (Exercise 7.3)
Explore 10 Videos
- TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:TRIANGLESExercise:SOLVED EXAMPLES
Explore 14 Videos
- STATISTICSBook:MTG IIT JEE FOUNDATIONChapter:STATISTICSExercise:Olympiad/HOTS Corner
Explore 20 Videos
Similar Questions
AB is a line segment D and P is its mid-point. D and E are points on the same side of AB such that ∠BAD=∠ABEand∠EPA=∠DPB (see figure). Show that

ΔDAP≅ΔEBP
View SolutionAB is a line segment and P is its midpoint. D and E are points on the same side of AD such that ∠BAD=∠ABEand∠EPA=∠DPB.
Show that (i) ΔDAP≅ΔEBP,
(ii)AD=BE.
View Solution
Knowledge Check
If C is the mid-point of AB and P is any point outside AB, then
APA + PB = PCBPA + PB + 2 PC = 0CPA + PB - 2PC = 0DPA + PB + PC = 0If C is the mid-point of AB and P is any point outside AB, then
APA+PB+PC=0BPA+PB+2PC=0CPA+PB=PCDPA+PB=2PC
AB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BE
View SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
ΔDAP≡ΔEBP
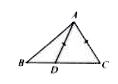
View SolutionD is a point on side BC of triangle ABC such that AD = AC (see figure). Show that AB>AD.
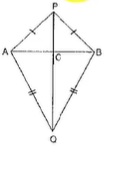
View SolutionAB is a line segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (in figure). Show that the line PQ is perpendicular bisector of AB
View SolutionD is a point on side BC of ΔABC such that AD=AC. Show that AB>AD.
View SolutionAB is a line-segment. P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (see Fig. 7.37). Show that the line PQ is the perpendicular bisector of AB
View Solution