ABCD is a trapezium in which AB I I DC. DC is produced to E such tha t CE= AB, prove that ar(ΔABD) = ar(ΔBCE).
To prove that the area of triangle ABD is equal to the area of triangle BCE in trapezium ABCD where AB is parallel to DC and CE = AB, we can follow these steps:
1. Identify the Trapezium:
We have trapezium ABCD with AB || DC. Extend DC to point E such that CE = AB.
2. Draw the Heights:
From point A, draw a perpendicular line to line DC. Let this perpendicular meet DC at point F. The length of this perpendicular is the height (h) of triangle ABD from vertex A to base DC.
3. Area of Triangle ABD:
The area of triangle ABD can be calculated using the formula:
AreaABD=12×base×height
Here, the base AB = x and the height from A to DC = h.
Therefore,
AreaABD=12×x×h
4. Draw the Heights for Triangle BCE:
Similarly, from point B, draw a perpendicular line to line CE. Let this perpendicular meet CE at point G. The length of this perpendicular is also the height (h) of triangle BCE from vertex B to base CE.
5. Area of Triangle BCE:
The area of triangle BCE can be calculated using the same area formula:
AreaBCE=12×base×height
Here, the base CE = AB = x (since CE = AB) and the height from B to CE = h.
Therefore,
AreaBCE=12×x×h
6. Equating the Areas:
Now we can equate the areas of triangles ABD and BCE:
AreaABD=12×x×h
AreaBCE=12×x×h
Thus,
AreaABD=AreaBCE
7. Conclusion:
Therefore, we have proved that the area of triangle ABD is equal to the area of triangle BCE.
We have trapezium ABCD with AB || DC. Extend DC to point E such that CE = AB.
From point A, draw a perpendicular line to line DC. Let this perpendicular meet DC at point F. The length of this perpendicular is the height (h) of triangle ABD from vertex A to base DC.
The area of triangle ABD can be calculated using the formula:
AreaABD=12×base×height
Here, the base AB = x and the height from A to DC = h.
Therefore,
AreaABD=12×x×h
Similarly, from point B, draw a perpendicular line to line CE. Let this perpendicular meet CE at point G. The length of this perpendicular is also the height (h) of triangle BCE from vertex B to base CE.
The area of triangle BCE can be calculated using the same area formula:
AreaBCE=12×base×height
Here, the base CE = AB = x (since CE = AB) and the height from B to CE = h.
Therefore,
AreaBCE=12×x×h
Now we can equate the areas of triangles ABD and BCE:
AreaABD=12×x×h
AreaBCE=12×x×h
Thus,
AreaABD=AreaBCE
Therefore, we have proved that the area of triangle ABD is equal to the area of triangle BCE.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Subjective Problems ) (Long Answer Type )
3 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Integer/Numerical Value Type )
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Subjective Problems ) (Very Short Answer Type )
9 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
Knowledge Check
In figure, ABCD is a trapezium in which AB I I DC. Find the length of DC.
 A17 cmB11 cmC13 cmD15 cm
A17 cmB11 cmC13 cmD15 cmIn the given figure, Here, ABCD is a parallellogram in which DC is extended to F such that AF intersects BC at E.
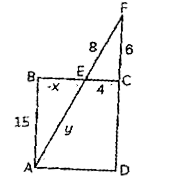
Perimeter of ΔABE=A35cmB36cmC40cmD45cm
ABCD is a trapezium with AB || DC.A parallel to AC cuts the line AB at X and BC at Y. Prove that ar (ADX) = ar (ACY)
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that

ar(ΔAEDF) = ar(ΔABCDE)
View SolutionA point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
View SolutionThe base BC of ΔABC is divided at D, so that BD=12DC.Prove that ar(ΔABD)=13ar(ΔABC)
View SolutionIn Fig. 4.123, ABCD is a trapezium with AB∣∣DC. If ΔAED is similar to ΔBEC, prove that AD=BC.
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solution
