A point E is taken on the side BC of a parallelogram ABCD. AE and DC are produced to meet at F. Prove that ar(ΔADF)=ar(ABFC).
Given ABCD is a parallelogram and E is a point on BC. AE and DC are produced to meet at F.
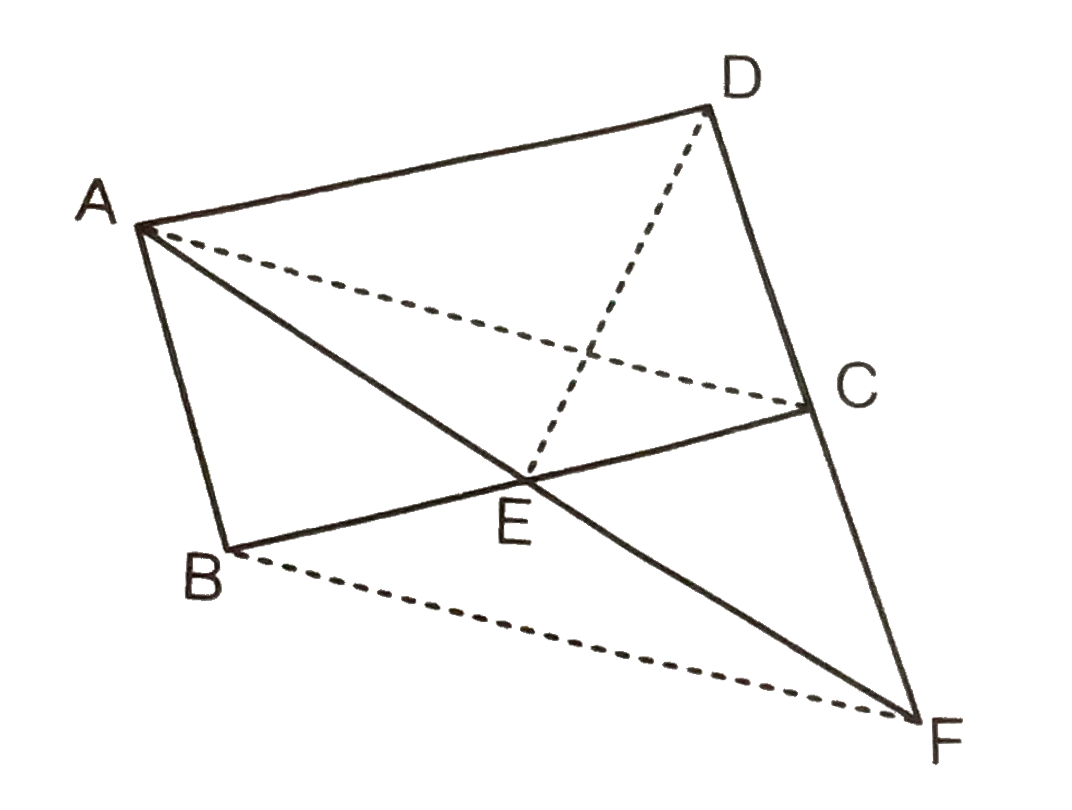
∴ AB||CDandBC||AD …(i)
To prove ar(ΔADF)=ar(ABFC)
Construction Join AC and DE.
Proof Since, AC is a diagonal of parallelogram ABCD.
So, ar(ΔABC)=ar(ΔACD) ...(ii)
Since, ΔABF and ΔABC are on the same base AB and between the same parallels AB and DF. [since, AB∣∣DC and DC produced to F ]
∴ ar(ΔABF)=ar(ΔABC) ...(iii)
From Eqs. (ii) and (iii).
ar(ΔABC)=ar(ΔACD)=ar(ΔABF)
On subtracting ar(ΔABE) from both sides of Eq. (iii), we get
ar(ΔABF)−ar(ΔABE)=ar(ΔABC)−ar(ΔABE)
⇒ ar(ΔBEF)=ar(ΔAEC) ...(iv)
Now, ar(AECD)=ar(ACD)+ar(AEC)
=ar(ΔABC)+ar(ΔBEF) [from Eqs. (ii) and (iv)]
On adding ar(ΔCEF) both sides, we get
ar(AECD)+ar(ΔCEF)
=ar(ΔABC)+ar(ΔBEF)+ar(ΔCEF)
⇒ ar(ΔADF)=ar(ABFC) Hence proved.
Topper's Solved these Questions
Similar Questions
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(i)DMMN=DCBN (ii)DNDM=ANDC
 View Solution
View SolutionIf E is a point on side AD produced of a parallelogram ABCD and BE intersects CD at F . Prove that DABE~DCFB .
View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
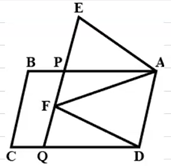
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
 View Solution
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that

ar(ΔAEDF) = ar(ΔABCDE)View SolutionDiagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
View SolutionP is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionE si a point on side AD produced of a parallelogram ABCD and BE intersects DC at F. prove that △ABE~△CFB.
View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
 View Solution
View Solution

