In the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that $a r (△ A D F) = a r (△ D C E)$ .

Video Solution

Answer

Step by step video & image solution for In the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar (triangleADF)=ar(triangleDCE). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Subjective Problems ) (Long Answer Type )
3 Videos
AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Integer/Numerical Value Type )
5 Videos
AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE ( Subjective Problems ) (Very Short Answer Type )
9 Videos
CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos

Knowledge Check

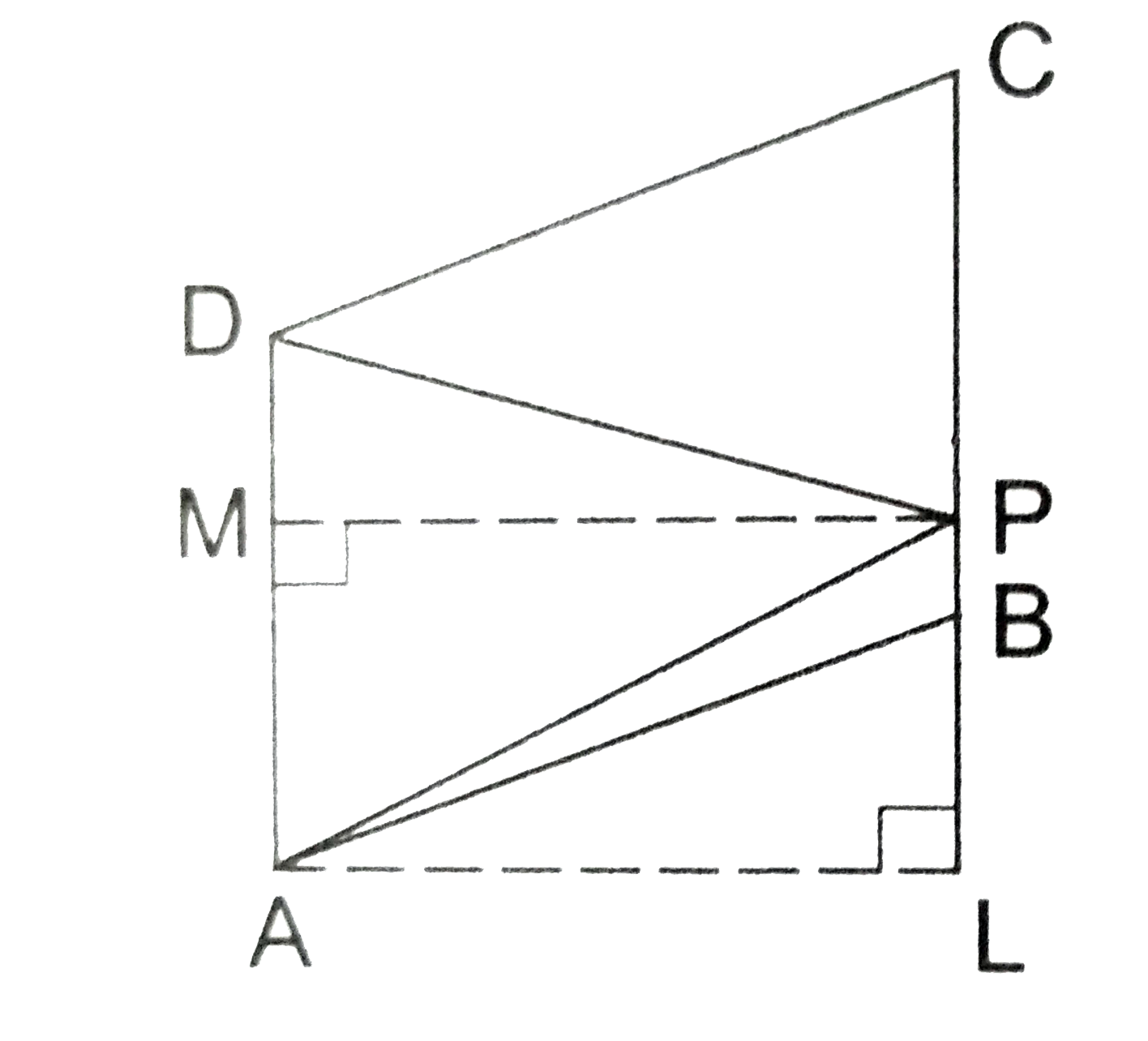
In the given figure, ABCD and AEFD a re two parallelograms.

ar( $Δ$ PEA) =
Aar( $∣ ∣^{g m} Δ$ PEA)
Bar( $Δ$ PFD)
Car( $Δ$ QFD)
Dar( $∣ ∣^{g m} Δ$ CQPB)

ABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that $a r (△ A X Y) = \frac{3}{8} a r (∣ ∣^{g m} A B C D)$
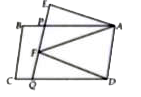
View Solution
In the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of $∠ B E F$ ?

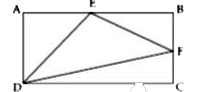
View Solution
In the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
$a r (△ A P Q) = a r (△ D P Q) = \frac{1}{6} a r (△ A B C D)$ .

View Solution
In the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View Solution
In the given figure ABCD is a trapezium with AB || DC. E and F are respectively midpoint of AD and BC. Prove that, $E F = \frac{1}{2} (A B + C D)$

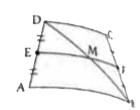
View Solution
In the given figure PSDA is a parallelogram in which PQ =QR= RS and AP II BQ II CR II VS.Prove that ar( $△ P Q E$ ) = ar( $△ D C F$ ).

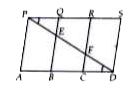
View Solution
P is any point on the diagonal BD of the parallelogram ABCD. Prove that ar $(△ A P D)$ = ar $(△ C P D)$ .
View Solution

MTG IIT JEE FOUNDATION-AREAS OF PARALLELOGRAMS AND TRIANGLES-EXERCISE ( Subjective Problems ) (Short Answer Type )

In Delta ABC, D is the mid-point of AB and P is any point on BC. If CQ...
03:28
ABCD is a trapezium in which AB I I DC. DC is produced to E such tha t...
02:29
Prove that the area of an equilateral triangle is equal to sqrt3/4 a^(...
05:30
In the given figure, ABCD is a parallelogram. E and F are any two poin...
03:38

Home
Ask Doubt
Profile

In the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).

Topper's Solved these Questions

Similar Questions

Knowledge Check

In the given figure, ABCD and AEFD a re two parallelograms. ar(ΔPEA) =

MTG IIT JEE FOUNDATION-AREAS OF PARALLELOGRAMS AND TRIANGLES-EXERCISE ( Subjective Problems ) (Short Answer Type )

In the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that $a r (△ A D F) = a r (△ D C E)$ .

In the given figure, ABCD and AEFD a re two parallelograms.

ar( $Δ$ PEA) =