ΔABCandΔDBC lie on the same side of BC, show in the figure. From a point on BC.PQ||ABandPR||BD are drawn, meeting AC at Q, and CD at R respectively. Prove that QA∣∣AD.
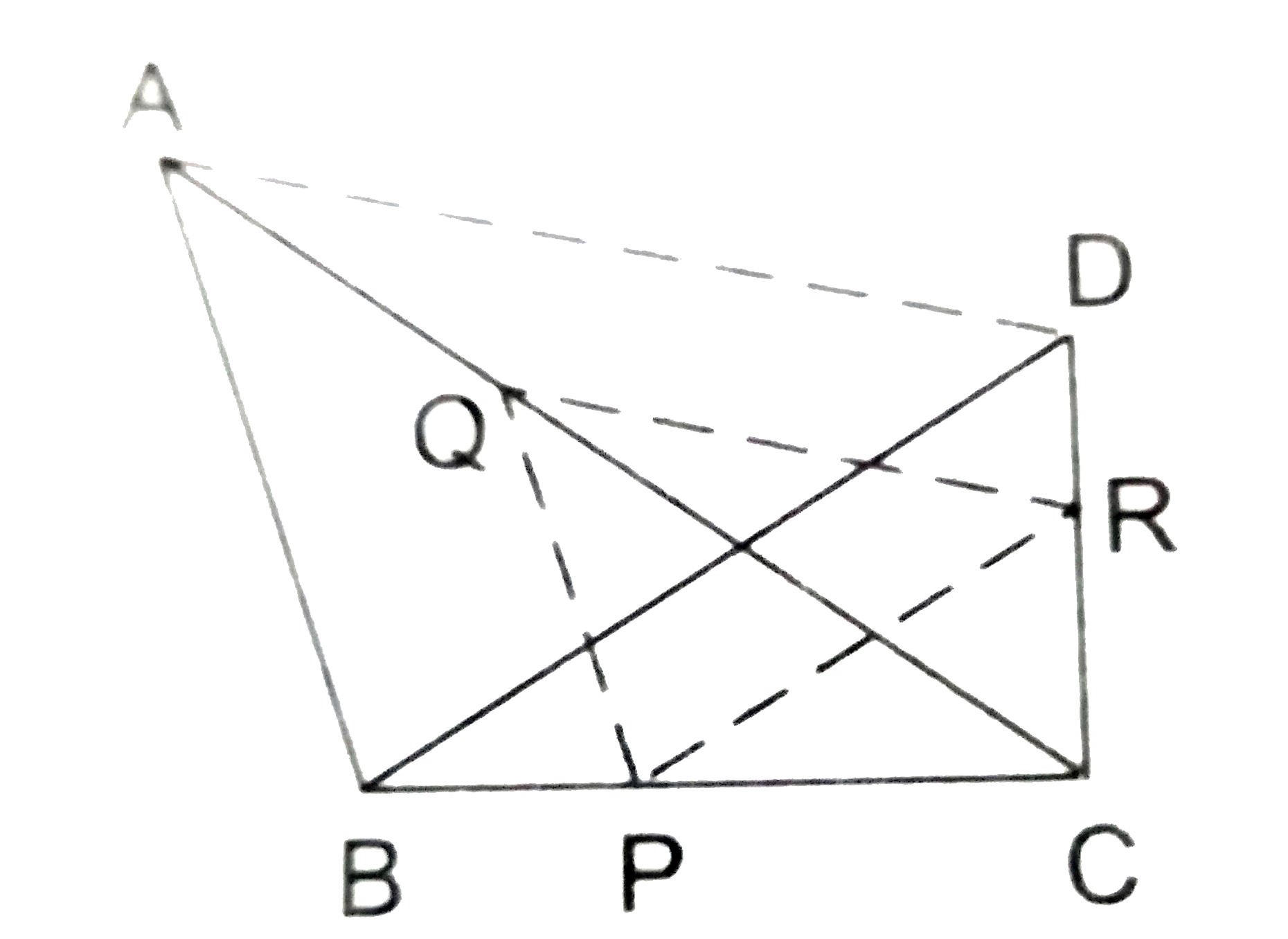
Step by step video & image solution for Delta ABC and Delta DBC lie on the same side of BC, show in the figure. From a point on BC.PQ||AB and PR||BD are drawn, meeting AC at Q, and CD at R respectively. Prove that QA||AD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.1
7 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.2
12 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner
15 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
Knowledge Check
Two right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
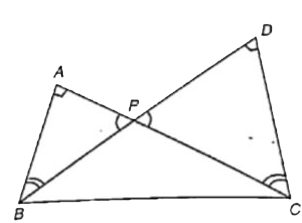 AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
AD is a median of ΔABC . The bisector of ∠ADB and ∠ADC meet AB and AC in E and F respectively. Prove that EF||BC
View SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View SolutionΔABCandΔDBC are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of ΔABC= area of ΔDBC
Prove that BC bisects the line segment AD.
View SolutionIn ΔABC, the bisector of ∠B meets AC at D. A line PQ∣∣AC meets AB,BC and BD at P,Q and R respectively. Show that BP×QR=BQ×PR.
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View Solution
