O is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
Step by step video & image solution for O is any point inside a rectangle ABCD. Prove that O B^2+O D^2=O A^2+O C^2. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.1
7 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.2
12 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner
15 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
O is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
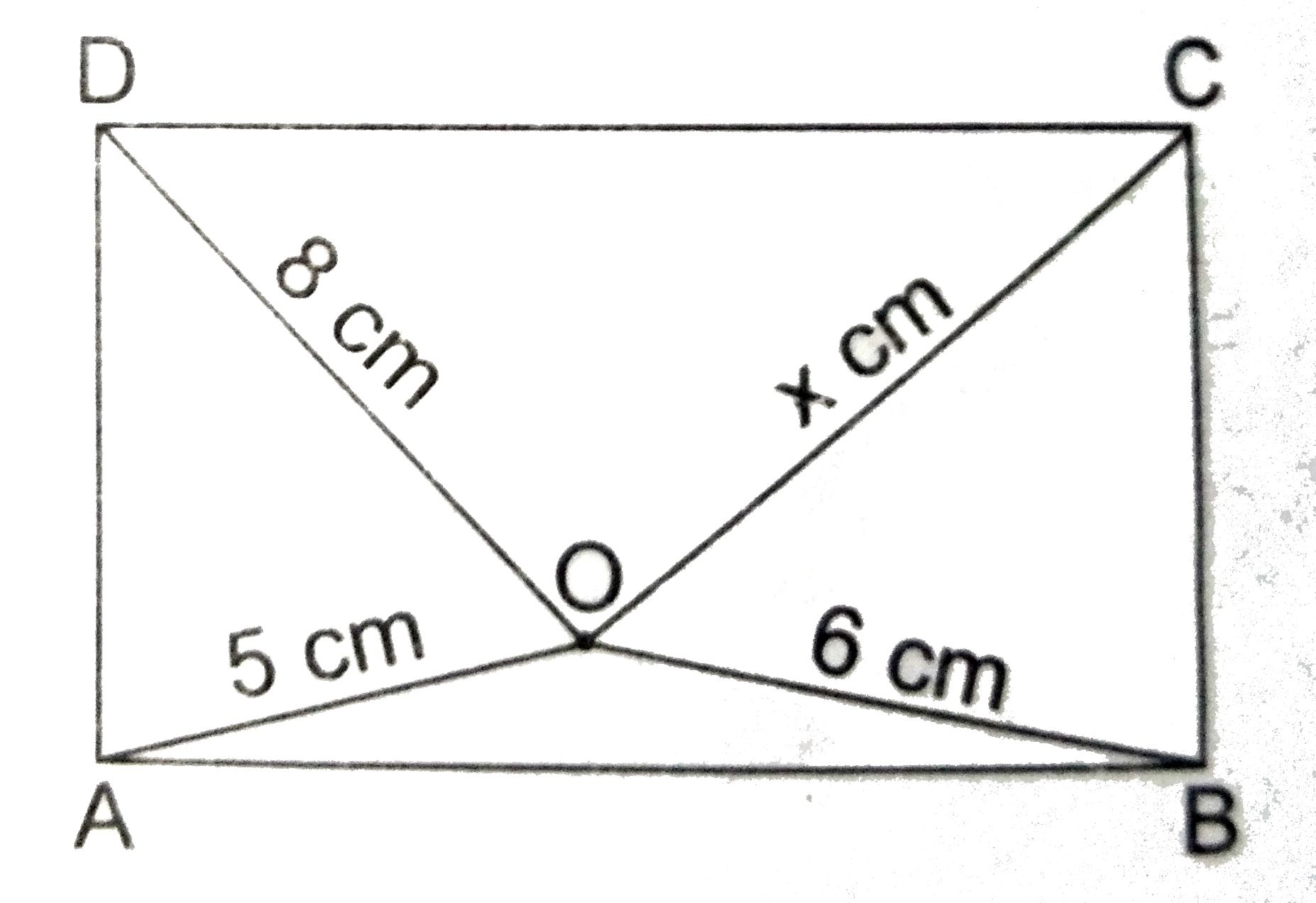
View SolutionA point O in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D . Prove that OB2+OD2=OC2+OA2
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionA point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. GIVEN : A rectangle ABCD and O is a point inside it. OA,OB,OC and OD have been joined.. TO PROVE : ar(AOD)+ar(BOC)=ar(AOB)+ar(COD) CONSTRUCTION : Draw EOFAB and LOMAD.
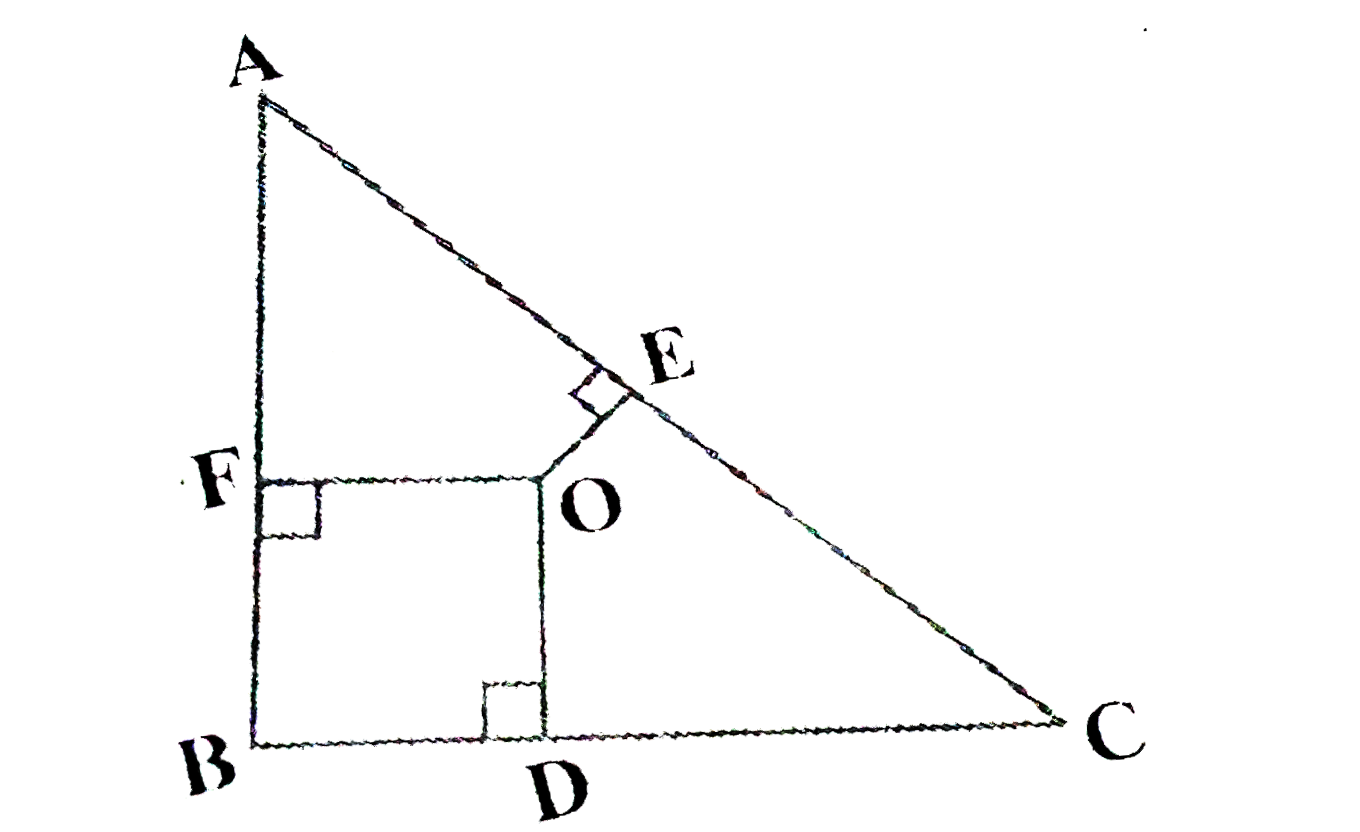
View SolutionIn fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionA point O inside a rectangle ABCD is joined to the vertices. Prove that the sum of the areas of a pair of opposite triangles so formed is equal to the sum of the other pair of triangles. Given: A rectangle ABCDandO is a point inside it. OA,OB,OCandOD have been joined. To Prove: ar(AOD)+ar(BOC)=ar(AOB)+ar(COD)
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View Solution
