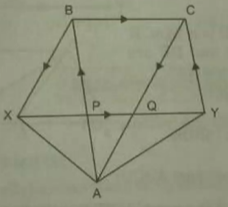
In Fig. 4.176, XYAC and XY divides triangular region ABC into two parts equal in area. Determine AXAB.
The correct Answer is:=√2−aSqrt(2)
Step by step video, text & image solution for In Fig. 4.176, X Y A C and X Y divides triangular region A B C into two parts equal in area. Determine (A X)/(A B)dot by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.1
7 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - NCERT Section Exercise 6.2
12 Videos
- TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner
15 Videos
- SURFACE AREAS AND VOLUMESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER
20 Videos
Similar Questions
Knowledge Check
Consider a region R={(x,y)∈R2:x2≤y≤2x}. If a line y=α divides the area of region R into two equal parts, then which of the following is true.?
Aα3−6α2+16=0B3α2−8α3/2+8=0Cα3−6α3/2−16D3α2−8α+8=0The area between x=y2and x=4 is divided into two equal parts by the line x=a, find the value of a.
Aa=723Ba=223Ca=523Da=423The figure shows a portion of the graph y=2x−4x3. The line y=c is such that the areas of the regions marked I and II are equal. If a, b are the x-coordinates of A,B respectively, then a+b equals-
 A2√7B3√7C4√7D5√7
A2√7B3√7C4√7D5√7
In Fig.76, ABCD. Find the value of x,y,z.
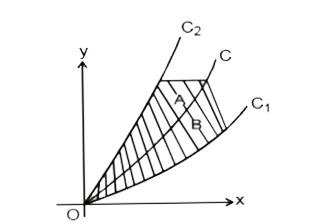
View SolutionLet C1andC2 be two curves passing through the origin as shown in the figure. A curve C is said to ‘‘bisect the area’’ the region between C1andC2, if for each point P of C, the two shaded regions A and B shown in the figure have equal areas. Determine the upper curve C2, given that the bisecting curve C has the equationy=x2 and that the lower curve C1 has the equation y=x2/2.
View SolutionThe area between the curve x=y2 and x=4 which divide into two equal parts by the line x=a. Find the value of a
View SolutionUsing integration find the area of the triangular region whose sides have equations y=2x+1, y=3x+1 and x=4
View SolutionUsing integration find the area of the triangular region whose sides have the equations y=2x+1, y=3x+1 and x=4.
View Solution