An object initially at rest explodes into three fragments $A, B$ and $C$ .The momentum of $A$ is $p \hat{i}$ and that of $B$ is $\sqrt{3} p \hat{j}$
where $p$ is $a + v e$ number. The momentum of $C$ will be

A

$(1 + \sqrt{3}) P$ in a direction making $120^{\circ}$ with A

B

2P in a direction making $150^{\circ}$ with A

C

2P in a direction making $150^{\circ}$ with B

D

$(1 + \sqrt{3}) P$ in a direction making $150^{\circ}$ with B

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Here $P_{x} = P and P_{y} = \sqrt{3} P$
$∴$ Resultant momentum of A and B
$P = \sqrt{P_{x}^{2} + P_{y}^{2}} = \sqrt{P^{2} + {(\sqrt{3} P)}^{2}} = 2 P$
It is along OC.
As is clear from figure

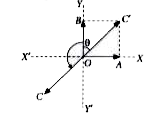
$\tan θ = \frac{B C .}{O B} = \frac{O A}{O B} = \frac{P}{\sqrt{3} P} = \frac{1}{\sqrt{3}}$ or $θ = 30^{\circ}$
As the object was initially at rest, the vector sum of linear momenta of A , B and C must be zero. Therefore, momentum of $C = 2 P$ along OC opposite to OC.. It takes an angle with $B = ∠ Y O C = ∠ Y O X . + ∠ X . O C = 90^{\circ} + 60^{\circ} = 150^{\circ}$

|

Updated on:21/07/2023

Class 9 PHYSICS FORCE AND LAWS OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An object initially at rest explodes into three fragments $A, B$ and $C$ .The momentum of $A$ is $p ˆ i$ and that of $B$ is $\sqrt{3} p ˆ j$
where $p$ is $a + v e$ number. The momentum of $C$ will be
A $(1 + \sqrt{3}) P$ in a direction making $120^{\circ}$ with A
B2P in a direction making $150^{\circ}$ with A
C2P in a direction making $150^{\circ}$ with B
D $(1 + \sqrt{3}) P$ in a direction making $150^{\circ}$ with B
Question 2 - Select One
An object , initially at rest , explodes into three fragments of equal mass . The momenta of two parts are $2 p ˆ i and p ˆ j$ where p is a positive number . The momentum of the third part is
AWill be of the magnitude 3p inclined at ${tan}^{- 1} (\frac{1}{2})$ with x - axis
BWill be of the magnitude $\sqrt{5} p$ inclined at ${tan}^{- 1} (2)$ with x - axis
CWill be of the magnitude 3p inclined at $π - {tan}^{- 1} (\frac{1}{2})$ with x - axis
DWill be of the magnitude $\sqrt{5} p$ inclined at $π + {tan}^{- 1} (\frac{1}{2})$ with x - axis
Question 3 - Select One
An object , initially at rest , explodes in three fragments. The momentum of two pieces are $- 3 p ˆ i$ and $- 4 p ˆ j$ where $p$ is a positive number. The momentum of the third piece
(i) will have magnitude $5 p$
(ii) will make an angle ${tan}^{- 1} (4 / 3)$ with the $x$ -axis
(iii) will make an angle ${tan}^{- 1} (3 / 4)$ with the $x$ -axis
(iv) will have magnitude $7 p$
A $(i), (i i i)$
B $(i), (i i)$
C $(i i), (i v)$
D $(i i i), (i v)$

MTG IIT JEE FOUNDATION-FORCE AND LAWS OF MOTION-EXERCISE (MULTIPLE CHOICE QUESTIONS)

Home
Ask Doubt
Profile