A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of level arm I. One force is of magnitude F and acts at one extreme end. The length of the rod is
malma+F
2(F+ma)lma
l(l+Fma)
(F+ma)l2ma
The correct Answer is:B
To solve the problem, we need to find the length of the rod (L) given the forces acting on it and the acceleration. Let's break down the solution step by step.
1. Understanding the Forces:
- We have a thin uniform rod of mass m.
- Two forces are acting on the rod:
- Force F acting at one extreme end.
- A second force F1 acting at the other end, which is greater than F.
- The lever arm (distance between the points where the forces are applied) is denoted as l.
2. Net Force and Acceleration:
- Since the rod is moving with a translational acceleration a, the net force acting on the rod can be expressed as:
F1−F=ma
- Rearranging gives us:
F1=F+ma
3. Torque Consideration:
- For the rod to have only translational motion and no rotational motion, the torques about the center of mass must balance out.
- The torque due to force F about the center of mass (which is at L/2) is:
τF=F⋅(L2)
- The torque due to force F1 is:
τF1=F1⋅(L2)
- Setting the torques equal gives us:
F⋅(L2)=F1⋅(L2−l)
4. Substituting F1:
- Substitute F1=F+ma into the torque equation:
F⋅(L2)=(F+ma)⋅(L2−l)
5. Solving for L:
- Expanding both sides:
F⋅L2=(F+ma)⋅(L2)−(F+ma)⋅l
- Rearranging gives:
F⋅L2−(F+ma)⋅L2=−(F+ma)⋅l
- Factor out L/2:
(F−(F+ma))⋅L2=−(F+ma)⋅l
- Simplifying:
−ma⋅L2=−(F+ma)⋅l
- Thus:
ma⋅L2=(F+ma)⋅l
- Solving for L:
L=2(F+ma)lma
6. Final Expression:
- Therefore, the length of the rod L is:
L=2(F+ma)lma
- We have a thin uniform rod of mass m.
- Two forces are acting on the rod:
- Force F acting at one extreme end.
- A second force F1 acting at the other end, which is greater than F.
- The lever arm (distance between the points where the forces are applied) is denoted as l.
- Since the rod is moving with a translational acceleration a, the net force acting on the rod can be expressed as:
F1−F=ma
- Rearranging gives us:
F1=F+ma
- For the rod to have only translational motion and no rotational motion, the torques about the center of mass must balance out.
- The torque due to force F about the center of mass (which is at L/2) is:
τF=F⋅(L2)
- The torque due to force F1 is:
τF1=F1⋅(L2)
- Setting the torques equal gives us:
F⋅(L2)=F1⋅(L2−l)
- Substitute F1=F+ma into the torque equation:
F⋅(L2)=(F+ma)⋅(L2−l)
- Expanding both sides:
F⋅L2=(F+ma)⋅(L2)−(F+ma)⋅l
- Rearranging gives:
F⋅L2−(F+ma)⋅L2=−(F+ma)⋅l
- Factor out L/2:
(F−(F+ma))⋅L2=−(F+ma)⋅l
- Simplifying:
−ma⋅L2=−(F+ma)⋅l
- Thus:
ma⋅L2=(F+ma)⋅l
- Solving for L:
L=2(F+ma)lma
- Therefore, the length of the rod L is:
L=2(F+ma)lma
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (MATCH THE FOLLOWING )2videos
FORCE AND LAWS OF MOTION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (ASSERTION AND REASON )10videos
FORCE AND LAWS OF MOTION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE MULTIPLE CHOICE QUESTIONS1videos
FORCE AND LAWS OF MOTION
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - Multiple Choice Question45videos
FOOTSTEPS TOWARDS NEET
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - GRAVITATION EXERCISE - Olympiad/HOTS Corner20videos
GRAVITATION
Similar Questions
A thin uniform rod of mass m=1kg moves translationally with acceleration a=2 ms−1 due to two antiparallel forces of arm-length l=20 cm . One forces is of magnitude 5 N and acts at one extreme end. Find the length of the rod.
 View Solution
View SolutionA thin uniform rod AB of mass m=1.0kg moves translationally with acceleration w=2.0m/s2 due to two antiparallel forces F1 and F2 (figure). The distance between the points at which these forces are applied is equal to a=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.
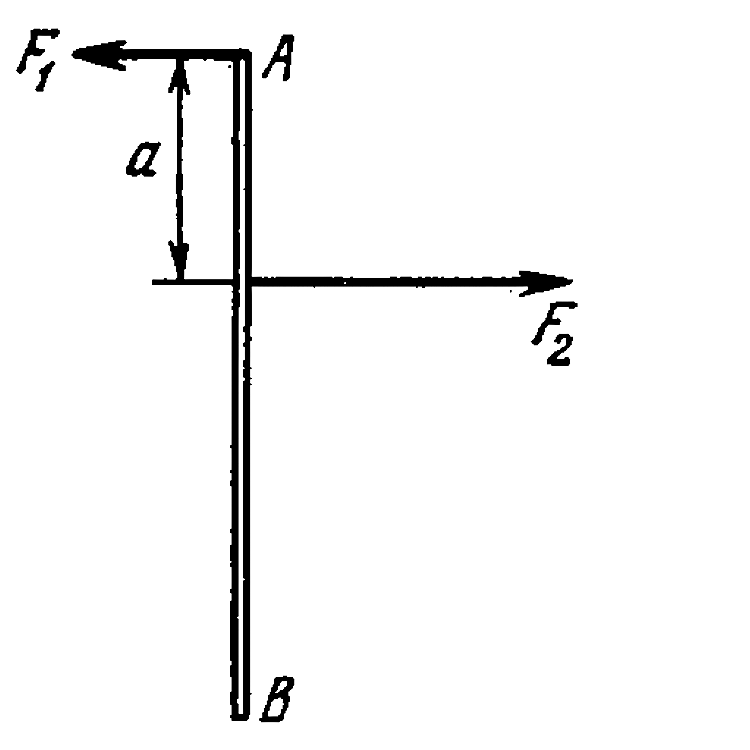 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A thin uniform rod of mass m moves translationally with acceleration a due to two antiparallel forces of lever arm l. One force is of magnitude F and acts at one extreme end. The length of the rod is
A2(F+ma)lmaBl(1+Fma)C(F+ma)l2maDmalma+F - Question 2 - Select One or More
A thin uniform rod AB of mass 1kg move translationally with acceleration a=2m/s2 due to two antiparallel force as shown. If l=20cm then:
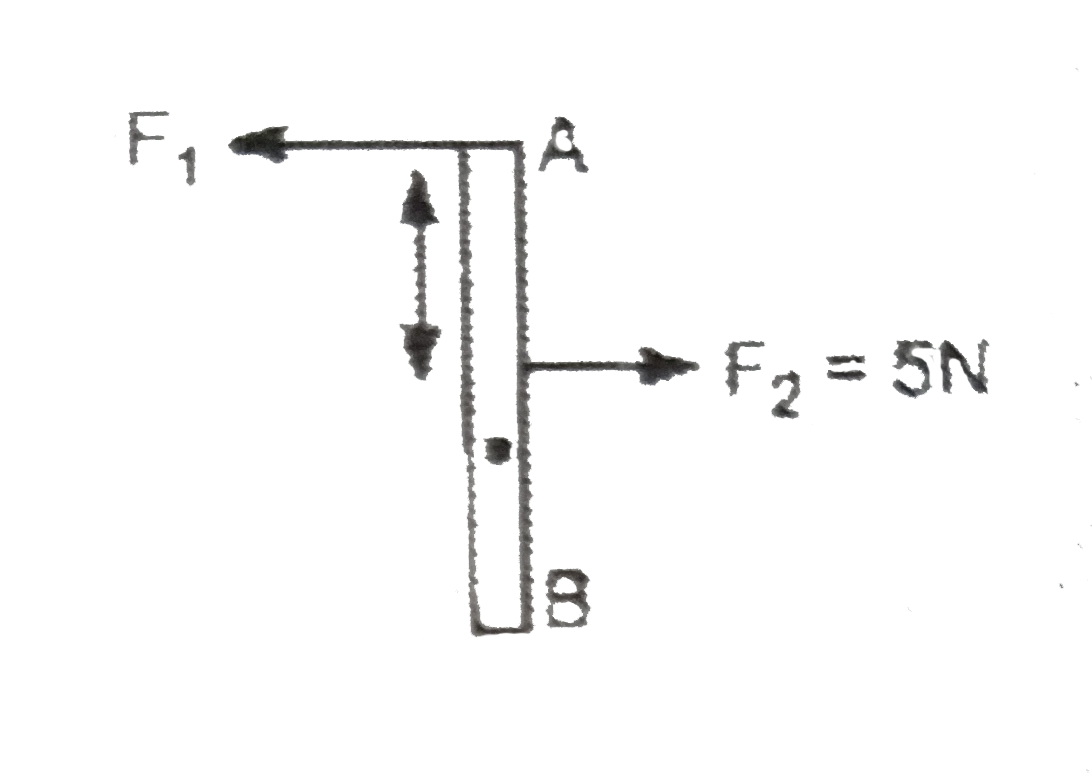 AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cm
AF1=3NBF1=5NCLength of rod is 1mDLength of rod is 80cm - Question 3 - Select One
A thin uniform rod AB of mass 1 kg moves translationally with acceleration a=2m/s2 due to two antiparallel forces F1 & F2. The distance between the points at which these forces are applied is equal to l=0.2m. If force F−(1)=8N then find the length of the rod in meter
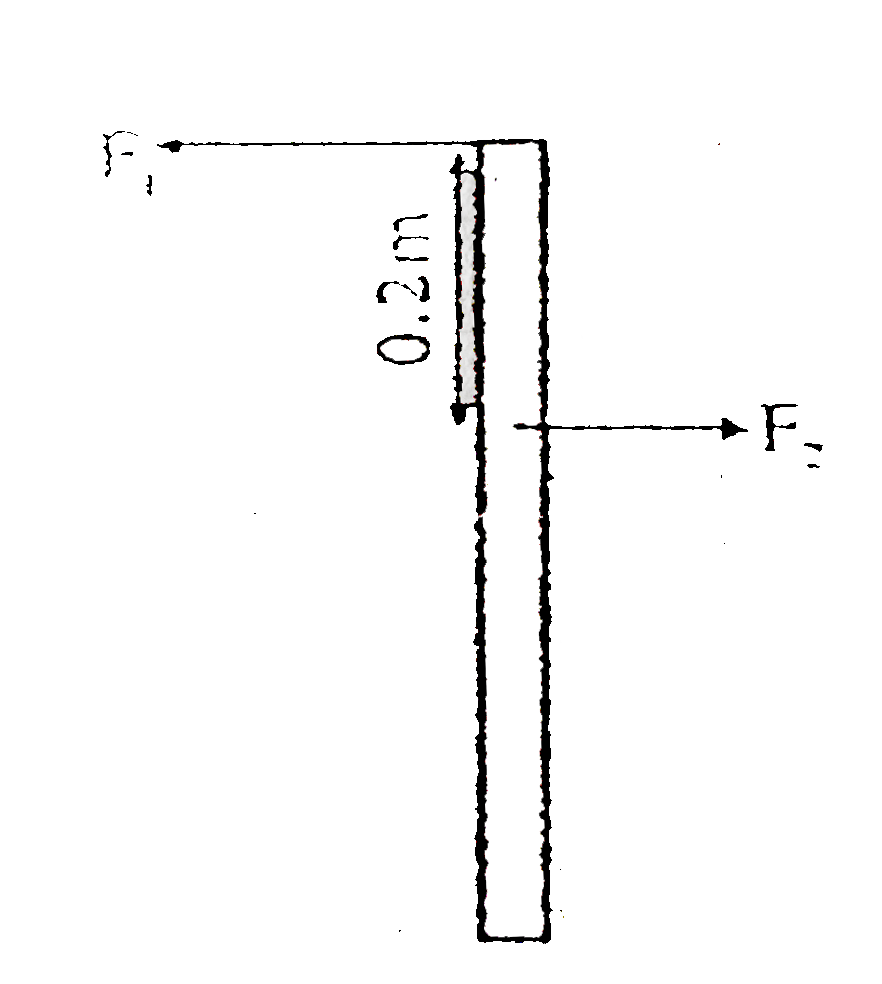 A1 mB2 mC3 mD4 m
A1 mB2 mC3 mD4 m
In the given figure, thin uniform rod AB of mass kg moves translationally with acceleration a=2ms^(2)due→twoantiparal≤lforcesF_(1) ,F_(2).Thedistancebetweenthep∮satwhichtheseforcesareappliedisequal→0.2 m.IfforceF_(1)=8 N, then find the length of the rod in meter.
'(##CEN_KSR_PHY_JEE_C09_E01_022_Q11##)'View SolutionA Thin uniform rod AB of mass m=1.0kg moves translationally with acceleration a=2.0m/s2 due to two antiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to d=20cm. Besides, it is known that F2=5.0N. Find the length of the rod.
 View Solution
View Solution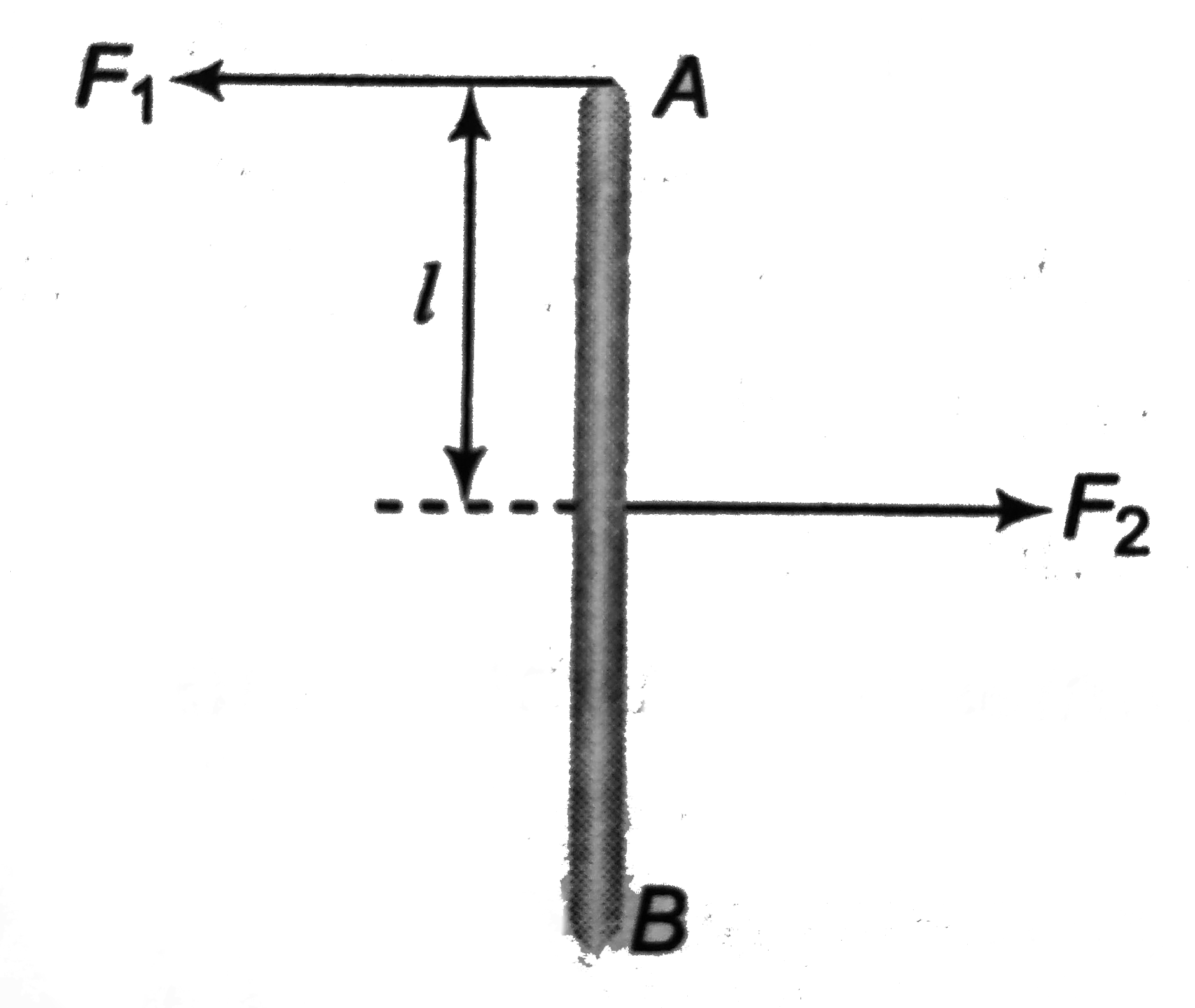
A thin uniform rod AB of mass m=1kg moves translationally with acceleration a=2m/s2 and to two anitiparallel forces F1 and F2. The distance between the points at which these forces are applied is equal to l=20cm besides it is known that F2=5N find the length of the rod.View SolutionA thin uniform rod AB of mass m and length L is placed on a smooth horizontal table. A constant horizontal force of magnitude F starts acting on the rod at one of the ends AB, Initially, the force is perpendicular to the length of the rod. Taking the moment at which force starts acting as t=0, find.
(a) Distance moved by centre of mass of the rod in time t0.
(b) Magnitude of initial acceleration of the end A of the rod.View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is
 View Solution
View Solution

