According to Newton second law of motion
F=m×v
f=m×a
f=ma
f=mv
The correct Answer is:B
Step-by-Step Solution:
1. Understanding Newton's Second Law of Motion:
Newton's second law states that the force acting on an object is equal to the rate of change of its momentum. Mathematically, this can be expressed as:
F∝dPdt
where F is the force, P is the momentum, and t is time.
2. Converting Proportionality to Equality:
To convert the proportionality into an equality, we introduce a constant of proportionality. In this case, we can express it as:
F=k⋅dPdt
By convention, we take k=1, leading to:
F=dPdt
3. Expressing Momentum:
The momentum P of an object is defined as the product of its mass m and its velocity v:
P=mv
Therefore, the change in momentum can be expressed as:
ΔP=P2−P1=mv2−mv1
4. Calculating Rate of Change of Momentum:
The rate of change of momentum with respect to time is given by:
dPdt=P2−P1t=mv2−mv1t
5. Substituting into the Force Equation:
Substituting the expression for the rate of change of momentum into the force equation gives:
F=mv2−mv1t
6. Simplifying the Expression:
Factoring out the mass m from the equation:
F=m⋅(v2−v1)t
The term (v2−v1)t represents acceleration a:
F=ma
7. Conclusion:
Thus, the mathematical statement of Newton's second law of motion is:
F=ma
This indicates that the force acting on an object is equal to the mass of the object multiplied by its acceleration.
8. Choosing the Correct Option:
Based on the derived equation F=ma, we can conclude that the correct option is the one that states F=ma.
---
Newton's second law states that the force acting on an object is equal to the rate of change of its momentum. Mathematically, this can be expressed as:
F∝dPdt
where F is the force, P is the momentum, and t is time.
To convert the proportionality into an equality, we introduce a constant of proportionality. In this case, we can express it as:
F=k⋅dPdt
By convention, we take k=1, leading to:
F=dPdt
The momentum P of an object is defined as the product of its mass m and its velocity v:
P=mv
Therefore, the change in momentum can be expressed as:
ΔP=P2−P1=mv2−mv1
The rate of change of momentum with respect to time is given by:
dPdt=P2−P1t=mv2−mv1t
Substituting the expression for the rate of change of momentum into the force equation gives:
F=mv2−mv1t
Factoring out the mass m from the equation:
F=m⋅(v2−v1)t
The term (v2−v1)t represents acceleration a:
F=ma
Thus, the mathematical statement of Newton's second law of motion is:
F=ma
This indicates that the force acting on an object is equal to the mass of the object multiplied by its acceleration.
Based on the derived equation F=ma, we can conclude that the correct option is the one that states F=ma.
Topper's Solved these Questions
- FORCE AND LAWS OF MOTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FORCE AND LAWS OF MOTIONEXERCISE - EXERCISE (INTEGER VALUE TYPE )
5 Videos
- FOOTSTEPS TOWARDS NEETBOOK - MTG IIT JEE FOUNDATIONCHAPTER - FOOTSTEPS TOWARDS NEETEXERCISE - Multiple Choice Question
45 Videos
- GRAVITATION BOOK - MTG IIT JEE FOUNDATIONCHAPTER - GRAVITATION EXERCISE - Olympiad/HOTS Corner
20 Videos
Similar Questions
When a body is moving uniformly along a straight line and there is no force of friction, acceleration/retardation of the body. According to Newton's second law of motion, the magnitude of force acting on a body is the product of mass and acceleration of the body
The distance - time table of an object in motion is given below
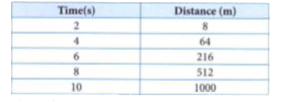
The force acting on the object
View SolutionWhen a body is moving uniformly along a straight line and there is no force of friction, acceleration/retardation of the body. According to Newton's second law of motion, the magnitude of force acting on a body is the product of mass and acceleration of the body
The distance - time table of an object in motion is given below

Which among the Newton's laws of motion can be used to calculate the force acting on the object in motion ?
View Solution
Knowledge Check
Assertion: Newton's second law of motion given the measurement of force.
Reason: According to Newton's second law of motion, force is directly proportional to the rate of change of momentum.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertion and reason are ture but reason is not the correct explanation of assertion.CIf assertion is ture but reason is false.DIf both assertion and reason are false.Assertion: Newton's second law of motion gives the measurement of force.
Reason: According to Newton's second law of motion, force is directly proportional to the rate of change of momentum.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are falseWhen a body is moving uniformly along a straight line and there is no force of friction, acceleration/retardation of the body. According to Newton's second law of motion, the magnitude of force acting on a body is the product of mass and acceleration of the body
The distance - time table of an object in motion is given below
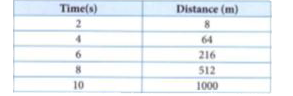
In the given table, acceleration of the object isAincreasingBdecreasingCconstantDnone of these
When a body is moving uniformly along a straight line and there is no force of friction, acceleration/retardation of the body. According to Newton's second law of motion, the magnitude of force acting on a body is the product of mass and acceleration of the body
The distance - time table of an object in motion is given below
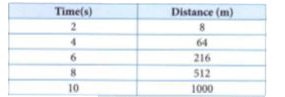
A passenger in a moving train tosses a coin which falls behind him. This shows that the motion of train is
View SolutionWhen a body is moving uniformly along a straight line and there is no force of friction, acceleration/retardation of the body. According to Newton's second law of motion, the magnitude of force acting on a body is the product of mass and acceleration of the body
The distance - time table of an object in motion is given below

Choose the correct order of the corresponding velocities of the object (in ms−1 ) in different time intervals .
View SolutionNewton's second law of motion is
View SolutionNewton's second law of motion is,
View SolutionNewton's second law of motion ______
View Solution
