1μmmg=_____Mmng
To solve the problem 1μmmg=?Mmng, we need to convert micrometers (µm) to megameters (Mm) and milligrams (mg) to nanograms (ng).
1. Convert micrometers to meters:
- We know that 1μm=10−6m.
- Therefore, 1μm=10−6m.
2. Convert meters to megameters:
- We know that 1Mm=106m.
- To convert meters to megameters, we divide by 106:
10−6m=10−6106Mm=10−12Mm.
3. Convert milligrams to grams:
- We know that 1mg=10−3g.
- Therefore, 1mg=10−3g.
4. Convert grams to nanograms:
- We know that 1ng=10−9g.
- To convert grams to nanograms, we multiply by 109:
10−3g=10−3×109ng=106ng.
5. Combine the conversions:
- Now we can substitute the converted values into the original expression:
1μmmg=10−12Mm106ng.
6. Simplify the expression:
- This simplifies to:
10−12106Mmng=10−12−6Mmng=10−18Mmng.
7. Final answer:
- Therefore, we have:
1μmmg=10−18Mmng.
Final Result:
1μmmg=10−18Mmng.
- We know that 1μm=10−6m.
- Therefore, 1μm=10−6m.
- We know that 1Mm=106m.
- To convert meters to megameters, we divide by 106:
10−6m=10−6106Mm=10−12Mm.
- We know that 1mg=10−3g.
- Therefore, 1mg=10−3g.
- We know that 1ng=10−9g.
- To convert grams to nanograms, we multiply by 109:
10−3g=10−3×109ng=106ng.
- Now we can substitute the converted values into the original expression:
1μmmg=10−12Mm106ng.
- This simplifies to:
10−12106Mmng=10−12−6Mmng=10−18Mmng.
- Therefore, we have:
1μmmg=10−18Mmng.
1μmmg=10−18Mmng.
Similar Questions
Knowledge Check
Assertion : A double convex lens (μ=1.5) has focal length 10cm. When the lens is immersed in water (μ=4/3) its focal length becomes 40cm.
Reason : 1f=μ1−μmμm(1R1−1R2)AIf both the assertion and reason are true and reason explains the assertion.BIf both the assertion and reason are true but reason does not explain the assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.Time taken by the sunlight to pass through a window made of glass of 5 mm thickness is __________ s.(μglass=1.5)
A2.5×10−11B0.4×10−8C4×10−8D2.5×10−5A spring block system is placed on a rough horizontal floor. The block is pulled towards right to give spring an eleongation less than 2μmgK but more than μmgK and released.
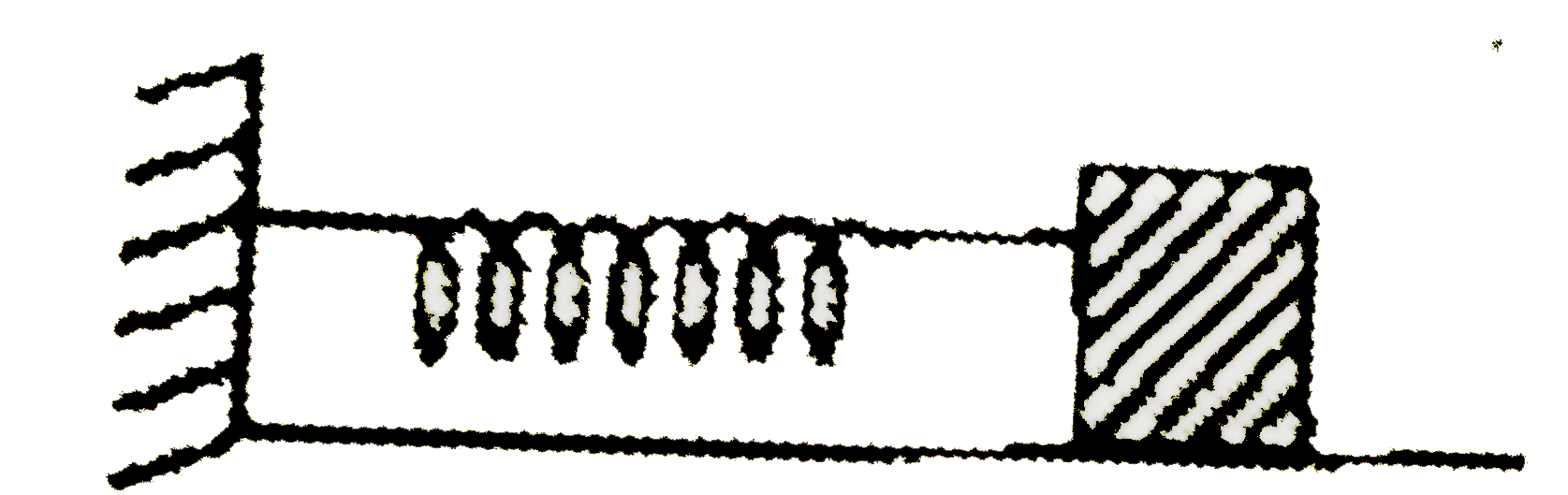
The correct statement is :AThe block will cross the mean positionBThe block will come to rest when the forces acting · on it are exactly balancedCThe block will come to rest when the work done by friction becomes equal to the change in energy stored in springDNone
Figure-2.85 shows a block B of mass m, cart C of mass M, and the coefficient of static between the block and the cart is μ. Neglect frictional between wheels and axles and the rotational effects of the wheels. Determine the minimum value of F which must be applied on B such that it will not slide.
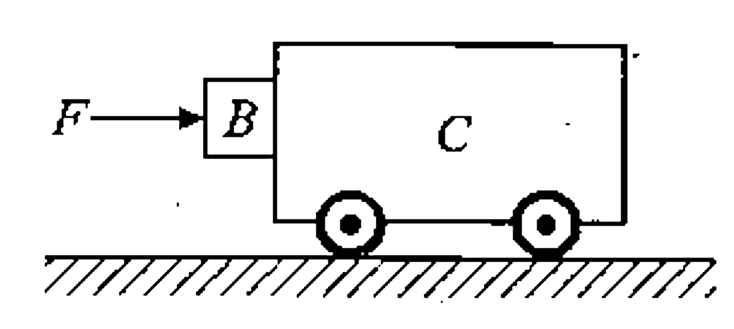
[mgμ(1+mM)]
View SolutionFor a two body oscillator system, prove the relation,
T=2π√μk
where, μ=m1m2m1+(m2)= reduced mass.
View SolutionShow that the force of attraction between two short magnets of moment m and m' with their centres d distance apart and their axes in the same direction along the same lines is μ04π6mm'd4
View SolutionTwo blocks of masses m1 and m2 kept touching each other on an inclined plane of inclination a with the horizontal. Show that (i) theforce of interaction between the blocks is (μ1−μ2)m1m2gcosα(m1+m2) and (ii) the minimum value of α at which the blocks just start sliding is a=tan−1.μ1m1+μ2m2m1+m2 . Where μ1 and μ2 are the coefficients of friction between the block m1 and the inclined plane and between the block m2 and the inclinedplane respectively.
View SolutionFind the accelerations of blocks A and B for the following cases.
(A) μ1=0 and μ2=0.1 (P)aA=aB=9.5m/s2
(B) μ2=0 and μ1=0.1 (Q)aA=9m/s2,aB=10m/s2
(C) μ1=0.1 and μ2=1.0 (R)aA=aB=g=10m/s2
(D) μ1=1.0 and μ2=0.1 (S)aA=1,aB=9m/s2
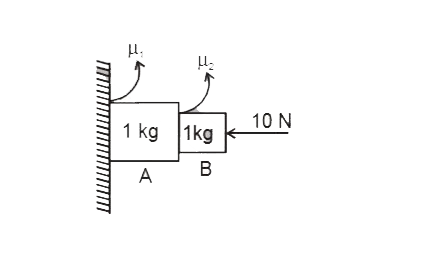
View Solution
