If M is the mid point of hypotenuse AC of rt. ΔABC then BM=12.....Solution in Punjabi
The correct Answer is:AC
Step by step video, text & image solution for If M is the mid point of hypotenuse AC of rt. DeltaABC then BM = 1/2..... by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABC is a triangle. Locate a point in the interior of ΔABC which is equidistant from all the vertices of ΔABC.
View SolutionTotal surface area of a cone = ..............
View SolutionABC is a right angled triangle with /_B= 90^@. M is the mid-point of AC and BM =sqrt117 .Sum of the length of other two sides AB and BC is 30. Then the value of 1/12 area of DeltaABC] is:
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View SolutionA (3,0,−1),B(2,10,6) and (1,2,1) are the vertices of a triangle. M is the mid point of the line segment joining AC and G is a point on line segment BM dividing 2:1 ratio internally find cos(∠GOA)
View SolutionIn ΔABC,∠B=90∘. If P is the mid-point of side AC, then
PA=PB=
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
D is the mid-point of AC
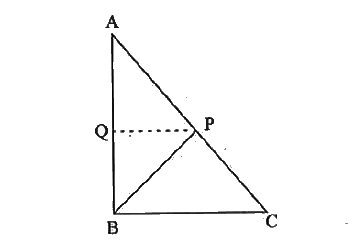
View Solutionयदि M समकोण ΔABC के कर्ण AC का मध्य बिंदु हो तो BM=12……………..
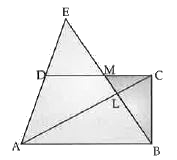
View SolutionThrought the mid-point M of the sides of a parallelogram ABCD, the line BM is drawn intersecting AC at L, and AD produced to E. Prove that EL=2BL.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD⊥AC (iii) CM=MA=12AB
View SolutionIf M is the mid point of hypotenuse AC of rt. ΔABC then BM=12.....
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that D is the mid-point of AC.
View SolutionABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that MD⊥AC.
View SolutionIn the adjoining figure, BM and CN are the altitudes drawn to the sides AC and AB respectively of ΔABC. If BM=CN, prove that ΔABC is isosceles.

View SolutionABC is a triangle right angled at C and M is mid-point of hypotenuse AB. Line drawn through M and parallel to BC intersects AC at D. Show that:
MD is mid-point of AC.
View Solution
