Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
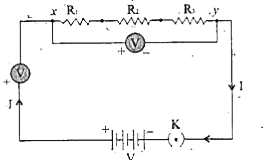
Let the potential difference across the resistors R1,R2andR3 are, V1,V2andV3 respectively. In the electric circuit shown above, let I be the current through the circuit. In this case, the current through each resistor is also I and the potential difference across a combination of resistors is equal to the sum of potential differences across this individual resistors. That is
V=V1+V2+V3 ....(1)
If the resistors R1,R2 and R3 are replaced by an equivalent single resistor R, such that the potential difference V across it, and current I through the circuit remain the same, then, applying the Ohm.s law to the entire circuit and three. resistors separately, we have
V=IR ...(2)
V1=IR1 ....(3)
V2=IR2
V3=IR3 .....(4)
By adding (3), (4) and (5), we get
V1+V2+V3=IR1+IR2+IR3
or V1+V2+V3(R1+R2+R3) .
By using equation (1)
V=I(R1+R2+R3)
By using equation (2)
IR=I(R1+R2+R3).
or R=R1+R1+R3
Similar Questions
3 resistors R1,R2andR3 are connected in series to a battery. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) Resistors are given as R1=10Ω,R2=20ΩandR3=30Ω. Calculate the effective resistance when they are connected in series . Also calculate the current flowing when the combination is connected to a 6V battery.
View SolutionThree resistors of resistances R1,R2andR3 are connected in (i) series and (ii) parallel. Write expression for the equivalent resistance of the combination in each case.
(b) Two identical resistance of 12Ω each are connected to a battery of 3V. Calculate the ratio of the power consumed by the resulting combinations with minimum resistance and maximum resistance.
View Solution
Knowledge Check
Tow resistance R1=50±2 ohm and R2=60 pm connected in series , the equivalent resistance of the series combination in
A(110±4) ohmB(110±2) ohmC(110±5) ohmD(110±6) ohmIn the circuit shown, n identical resistors R are connected in parallel (n gt 1) and the combination is connected in series to another resistor R0. In the adjoining circuit n resistors of resistance R are all connected in series along with R0–
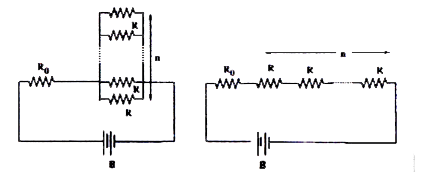
The batteries in both circuits are identical and net power dissipated in the n resistors in both circuits is same. The ratio R0/R isA1BnCn2D1/nTwo resistors of resistance R1 and R2 having R1>R2 are connected in parallel. For equivalent resistance R, the correct statement is
AR>R1+R2BR1<R<R2CR2<R<(R1+R2)DR<R1
Show by a diagram how two resistors R1andR2 are joined in parallel. Obtain an expression for the total resistance of the combination.
View SolutionTwo coils of resistances R1=3ΩandR2=6.Ωare connected in series across a battery of p.d. 12 V. Draw the circuit diagram. Find :
the total electrical energy supplied by the battery in 1 minute.
View SolutionTwo resistors R1andR2 of resistance 3 Ω and 6 Ωrespectively are connected in parallel across a battery of p.d. 12 V. Draw the circuit diagram. Calculate the electrical energy consumed in 1 minute in each resistance.
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View Solution
