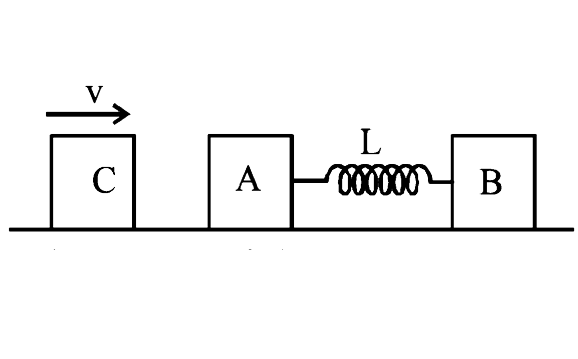
Two identical blocks A and B, each of mass m resting on a smooth floor are connected by a light spring of natural length Land spring constant K, with the spring in its natural length. A third identical block of mass m moving with a speed v along the line joining Aand B collides with A. The maximum compression in the spring is
v√m2K
m√v2K
√mKv
mv2K
The correct Answer is:A
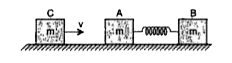
Because the masses of A and Care identical and, initially the body A is not in motion, hence when the body .C. collides elastically to body A, it itself gets stopped and transfers its momentum ‘mv.and K.E.(1/2m2) totally to body A. In this position, B is stationary, and spring is in its normal state. Hence, the instantaneous momentum of the system is my and KE is 1/2mv2. Now, the spring is compressed and block B also comes in motion. Suppose the instantaneous velocity of A and B after the collision be v2 and compression of the spring is x.As no external force acts on the system, we have according to law of conservation of momentum and energy,
mv=mv.+mv. or v=2v.(1)
Also , 12mv2=12mv2+12mv.2+12Kx2 or v2=2v.2+Kx2m
From eqn. (1) v.=v2∴v2=v22+Kx2m
or kx2m=v22 or x=v√m2K.
Similar Questions
Two blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 View Solution
View SolutionTwo identical blocks A and B each of mass m resting on the smooth horizontal floor are connected by a light spring of natural length L and spring constant K. A third block Cof mass m moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
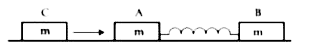 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBv√v2kC√mvkDmv2k - Question 2 - Select One
Two identical blocks A and B , each of mass m resting on smooth floor are connected by a light spring of natural length L and spring constant k, with the spring at its natural length. A third identical block C (mass m) moving with a speed v along the line joining A and B collides with A. The maximum compression in the spring is
Av√m2kBm√m2kC√mvkDmv2k - Question 3 - Select One or More
Two blocks A and B, each of mass m, are connected by a masslesss spring of natural length L and spring constant K. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown in fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B, and collides elastically with A. Then
 Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
Athe kinetic energy of the A-B system, at maximum compression of the spring, is zero.Bthe kinetic energy of the A-B system, at maximum compression of the spring, is mv2/4.Cthe maximum compression of the spring is v√(m/K)Dthe maximum compression of the spring is v√(m/2K)
Two blocks A and B each of mass m are connected by a massless spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length. A third identical block C also of mass m moves on the floor with a speed v along the line joining A and B and collides with A. Then
The kinetic energy of the A-B system at maximum compression of the spring is mv2/4
The maximum compression of the spring v√m/3k<br>Thek∈etice≠rgyoftheA−Bsystematmaxiμmcompression<br>Themaxiμmcoppressionofthespr∈gisvsqrt(m//k)View SolutionTwo blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -
 View Solution
View SolutionTwo blocks A and B of masses m and 2m are connected by a massless spring of natural length L and spring constant k. The blocks are intially resting on a smooth horizontal floor with the spring at its natural length , as shown . A third identical block C of mass m moves on the floor with a speed v0 along the line joining A and B and collides elastically with A. FInd (a) the velocity of c.m. of system (blockA+B+spring) and (b) the minimum compression of spring.
 View Solution
View SolutionTwo blocks A and B. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 View Solution
View SolutionTwo blocks A and H. each of mass m, are connected by a massless spring of natural length I. and spring constant K. The blocks are initially resting in a smooth horizontal floor with the spring at its natural length, as shown in Fig. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A and B. and collides elastically with A. Then
 View Solution
View Solution

