Which of the following points will be collinear with the points (-3, 4) and (2, -5) ?
(0, 0)
(7, -14)
(0, -1)
(3, 1)
The correct Answer is:B
To determine which of the given points is collinear with the points (-3, 4) and (2, -5), we will first find the equation of the line that passes through these two points.
1. Identify the Points:
The two points we have are:
- Point A: (-3, 4)
- Point B: (2, -5)
2. Find the Slope (m):
The slope m of the line passing through two points (x1,y1) and (x2,y2) is given by the formula:
m=y2−y1x2−x1
Substituting the values:
m=−5−42−(−3)=−95=−95
3. Use Point-Slope Form to Find the Equation of the Line:
The point-slope form of the equation of a line is:
y−y1=m(x−x1)
Using point A (-3, 4):
y−4=−95(x+3)
Simplifying this, we get:
y−4=−95x−275
y=−95x+4−275
y=−95x+205−275
y=−95x−75
4. Check Each Point for Collinearity:
We will check each of the given options to see if they satisfy the line equation y=−95x−75.
- Option A: (0, 0):
y=−95(0)−75=−75(Not collinear)
- Option B: (7, -14):
y=−95(7)−75=−635−75=−705=−14(Collinear)
- Option C: (0, -1):
y=−95(0)−75=−75(Not collinear)
- Option D: (3, 1):
y=−95(3)−75=−275−75=−345(Not collinear)
5. Conclusion:
The only point that is collinear with the points (-3, 4) and (2, -5) is Option B: (7, -14).
The two points we have are:
- Point A: (-3, 4)
- Point B: (2, -5)
The slope m of the line passing through two points (x1,y1) and (x2,y2) is given by the formula:
m=y2−y1x2−x1
Substituting the values:
m=−5−42−(−3)=−95=−95
The point-slope form of the equation of a line is:
y−y1=m(x−x1)
Using point A (-3, 4):
y−4=−95(x+3)
Simplifying this, we get:
y−4=−95x−275
y=−95x+4−275
y=−95x+205−275
y=−95x−75
We will check each of the given options to see if they satisfy the line equation y=−95x−75.
y=−95(0)−75=−75(Not collinear)
y=−95(7)−75=−635−75=−705=−14(Collinear)
y=−95(0)−75=−75(Not collinear)
y=−95(3)−75=−275−75=−345(Not collinear)
The only point that is collinear with the points (-3, 4) and (2, -5) is Option B: (7, -14).
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - TEST YOURSELF15videos
COORDINATE GEOMETRY
- BOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - STANDARD LEVEL46videos
COORDINATE GEOMETRY
- BOOK - DISHA PUBLICATIONCHAPTER - AVERAGESEXERCISE - Test Yourself15videos
AVERAGES
- BOOK - DISHA PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Test Yourself15videos
FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following points are collinear ?
A(2a,0),(3a,0),(a,2a)B(3a,0),(0,3b),(a,2b)C(3a,b),(a,2b),(−a,b)D(a,−6),(−a,3b),(−2a,−2b) - Question 2 - Select One
Which of the following points are collinear ?
A(-2,3),(3,-1) and (-7,5)B(-1,1) ,(5,7) and (8,10)C(-3,-1),(1,-2) and (6,2)D(0,1) ,(3,0) and(-1,-3) - Question 3 - Select One
Which of the following set of points are collinear?
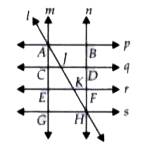 AA.J.K.HBA.J.E.GCB.D. H. EDA.J. K. F
AA.J.K.HBA.J.E.GCB.D. H. EDA.J. K. F
The locus of a point which is collinear with the points (1,2) and (−2,1) is
View SolutionThe locus of a point which is collinear with the points A(2,3) and B(3,2) .is
View SolutionThe locus of a point collinear with two given points (2,4) and (6,8).
View Solution" The locus of a point which is collinear with the points "A(3,4)B(4,3)" is "
View SolutionWhich of the following set of points are non-collinear?
View Solution

