The middle point of A (1, 2) and B (x, y) is C (2, 4). If BD is perpendicular to AB such that CD = 3 unit, then what is the length BD ?
2√2 unit
2unit
3 unit
3√2 unit
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Find the coordinates of point B
We know that point C is the midpoint of points A (1, 2) and B (x, y). The formula for the midpoint C is given by:
C(x1+x22,y1+y22)
Substituting the coordinates of A and C into the formula:
C(2,4)=(1+x2,2+y2)
This gives us two equations:
1. 1+x2=2
2. 2+y2=4
Step 2: Solve for x
From the first equation:
1+x2=2
Multiplying both sides by 2:
1+x=4
Subtracting 1 from both sides:
x=3
Step 3: Solve for y
From the second equation:
2+y2=4
Multiplying both sides by 2:
2+y=8
Subtracting 2 from both sides:
y=6
Thus, the coordinates of point B are (3, 6).
Step 4: Find the length of BC
Now that we have the coordinates of B (3, 6) and C (2, 4), we can find the distance BC using the distance formula:
BC=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of B and C:
BC=√(3−2)2+(6−4)2
Calculating:
BC=√(1)2+(2)2=√1+4=√5
Step 5: Use Pythagorean theorem to find BD
We know that BD is perpendicular to AB, and CD = 3 units. We can apply the Pythagorean theorem in triangle BCD:
CD2=BD2+BC2
Substituting the known values:
32=BD2+(√5)2
Calculating:
9=BD2+5
Step 6: Solve for BD
Rearranging the equation:
BD2=9−5
BD2=4
Taking the square root:
BD=√4=2
Final Answer
The length of BD is 2 units.
---
We know that point C is the midpoint of points A (1, 2) and B (x, y). The formula for the midpoint C is given by:
2. 2+y2=4
From the first equation:
From the second equation:
Now that we have the coordinates of B (3, 6) and C (2, 4), we can find the distance BC using the distance formula:
We know that BD is perpendicular to AB, and CD = 3 units. We can apply the Pythagorean theorem in triangle BCD:
Rearranging the equation:
BD2=4
The length of BD is 2 units.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - TEST YOURSELF15videos
COORDINATE GEOMETRY
- BOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - STANDARD LEVEL46videos
COORDINATE GEOMETRY
- BOOK - DISHA PUBLICATIONCHAPTER - AVERAGESEXERCISE - Test Yourself15videos
AVERAGES
- BOOK - DISHA PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Test Yourself15videos
FUNCTIONS
Similar Questions
In the figure given below, ABC is a triangle with AB perpendicular to BC. Further BD is perpendicular to AC. If AD = 9 cm and DC = 4 cm, then what is the length of BD ?
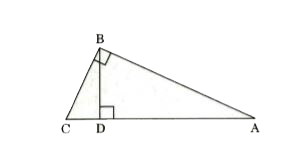 View Solution
View SolutionIf the points A(1,3), B(−2,1), C(x,2) and D(−1,5) are given and AB is perpendicular to CD, find the value of x.
View Solution
Knowledge Check
- Question 1 - Select One
Suppose AB is a diameter of a circle, whose centre is at O and C be any point on the circle. If CD is perpendicular to AB and CD = 12 cm, AD = 16 cm, then BD is equal to
A10 cmB12 cmC8 cmD9 cm - Question 2 - Select One
In ΔABC,ifAC=8,BC=7 and D lies between A and B such that AD=2,BD=4, then the length CD equals
A√46B√48C√51D√75 - Question 3 - Select One
In ΔABC,∠C=90∘ and CD is perpendicular to AB at D. If ADBD=√k, then ACBC=?
Aa)kBb)√kCc)1√kDd)4√k
In a triangle ABC, ∠B=90∘,AB=8cm,BC=6cm. BD is perpendicular to AC, then find the length of CD, AD and BD.
View SolutionIn a triangle ABC, ∠BCA=90∘ and CD is perpendicular to AB. If AD = 4 cm and BD = 9 cm, then the value of DC will be
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View SolutionIn ΔABC, we have AC=BC=7andAB=2. Suppose that D is a point on line AB such that B lies between A and D and CD=8. What is the length of the segment BD?
View SolutionIn an equilateral triangle ABC, BD is drawn perpendicular to AC. What is BD2 equal to ?
View Solution

