(3,- 4) and (5, -2) are two consecutive vertices of a square in which (2, -2) is an interior point. The centre of the square is at

(1, 2)
(3, - 2)
(0, 2)
(4, - 2)
The correct Answer is:B
Step by step video, text & image solution for (3,- 4) and (5, -2) are two consecutive vertices of a square in which (2, -2) is an interior point. The centre of the square is at by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - TEST YOURSELF15videos
COORDINATE GEOMETRY
- BOOK - DISHA PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - STANDARD LEVEL46videos
COORDINATE GEOMETRY
- BOOK - DISHA PUBLICATIONCHAPTER - AVERAGESEXERCISE - Test Yourself15videos
AVERAGES
- BOOK - DISHA PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Test Yourself15videos
FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
If the points ( k, k -1) , (k + 2 , k + 1) and (k , k +3) are three consective vertices of a square , then its area (in square units ) is _______.
A2B4C8D6 - Question 2 - Select One
If the ratio of diagonals of two squares is 3:2 then the ratio of the areas of two squares is :
A4:5B6:5C9:4D√3:√2
If (2,1),(−2,5) are two opposite vertices of a square; then the area of the square is
View SolutionTwo opposite vertices of a square are (−1, 2) and (3, 2) . Find the coordinates of other two vertices.
View SolutionThe two opposite vertices of a square are (−1,2) and (3,2). Find the coordinates of the other two vertices.
View SolutionPoint charges q and -q located at the vertices of a square with diagonals 2l as shown in figure. Find the magnitude of the electric field at a point located symmetrically with respect to the vertices of the square at a distance x from its centre. Consider x>>l0
[−ql√2πε0x3]
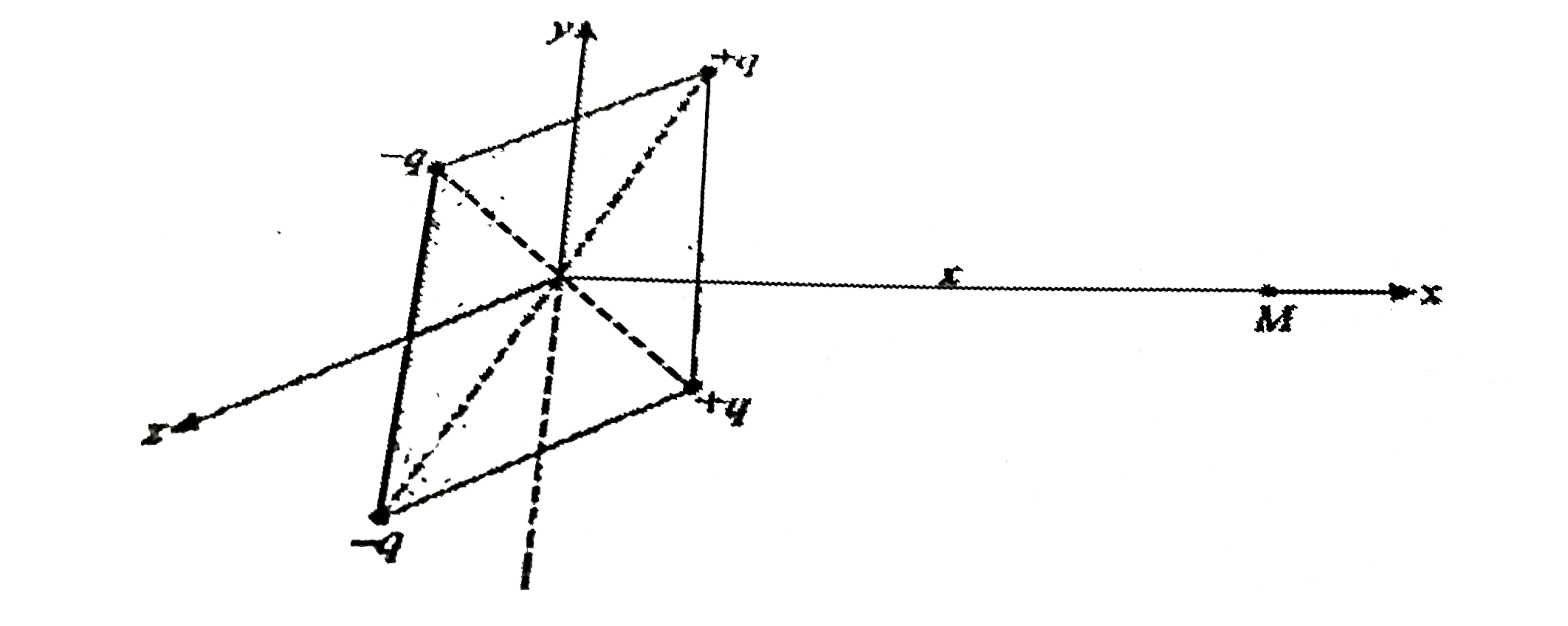 View Solution
View SolutionTwo adjacent vertices of a square are (1, 2) and (−2,6) Find the other vertices.
View SolutionQ.7 The two opposite vertices of a square are (l.-6)and (5,4). Find the coordinates of the other two vertices.
View Solution

