What will be the area of the rhombus ax±by±c=0 ?
(3c2)/(ab)
(4c2)/(ab)
(2c2)/(ab)
(c2)/(ab)
The correct Answer is:C
To find the area of the rhombus represented by the equation ax+by+c=0, we can follow these steps:
Step 1: Identify the equations of the lines
The rhombus is formed by the following four lines:
1. ax+by+c=0
2. ax+by−c=0
3. ax−by+c=0
4. ax−by−c=0
Step 2: Find the points of intersection
We need to find the intersection points of these lines to determine the vertices of the rhombus.
- For the first line ax+by+c=0:
- Set x=0 to find the y-intercept:
y=−cb(Point: (0,−cb))
- Set y=0 to find the x-intercept:
x=−ca(Point: (−ca,0))
- For the second line ax+by−c=0:
- Set x=0:
y=cb(Point: (0,cb))
- Set y=0:
x=ca(Point: (ca,0))
- For the third line ax−by+c=0:
- Set x=0:
y=cb(Point: (0,cb))
- Set y=0:
x=−ca(Point: (−ca,0))
- For the fourth line ax−by−c=0:
- Set x=0:
y=−cb(Point: (0,−cb))
- Set y=0:
x=ca(Point: (ca,0))
Step 3: Identify the vertices of the rhombus
From the points calculated, we have the vertices of the rhombus as:
1. (0,cb)
2. (0,−cb)
3. (ca,0)
4. (−ca,0)
Step 4: Calculate the lengths of the diagonals
The lengths of the diagonals D1 and D2 can be calculated as follows:
- D1 (vertical diagonal) is the distance between (0,cb) and (0,−cb):
D1=∣∣∣cb−(−cb)∣∣∣=2cb
- D2 (horizontal diagonal) is the distance between (ca,0) and (−ca,0):
D2=∣∣ca−(−ca)∣∣=2ca
Step 5: Calculate the area of the rhombus
The area A of the rhombus can be calculated using the formula:
A=12×D1×D2
Substituting the values of D1 and D2:
A=12×(2cb)×(2ca)=2c2ab
Final Answer
Thus, the area of the rhombus is:
Area=2c2ab
The rhombus is formed by the following four lines:
1. ax+by+c=0
2. ax+by−c=0
3. ax−by+c=0
4. ax−by−c=0
We need to find the intersection points of these lines to determine the vertices of the rhombus.
- Set x=0 to find the y-intercept:
y=−cb(Point: (0,−cb))
- Set y=0 to find the x-intercept:
x=−ca(Point: (−ca,0))
- Set x=0:
y=cb(Point: (0,cb))
- Set y=0:
x=ca(Point: (ca,0))
- Set x=0:
y=cb(Point: (0,cb))
- Set y=0:
x=−ca(Point: (−ca,0))
- Set x=0:
y=−cb(Point: (0,−cb))
- Set y=0:
x=ca(Point: (ca,0))
From the points calculated, we have the vertices of the rhombus as:
1. (0,cb)
2. (0,−cb)
3. (ca,0)
4. (−ca,0)
The lengths of the diagonals D1 and D2 can be calculated as follows:
- D1 (vertical diagonal) is the distance between (0,cb) and (0,−cb):
D1=∣∣∣cb−(−cb)∣∣∣=2cb
D2=∣∣ca−(−ca)∣∣=2ca
The area A of the rhombus can be calculated using the formula:
A=12×D1×D2
Substituting the values of D1 and D2:
A=12×(2cb)×(2ca)=2c2ab
Thus, the area of the rhombus is:
Area=2c2ab
Topper's Solved these Questions
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:TEST YOURSELF
Explore 15 Videos
- COORDINATE GEOMETRYBook:DISHA PUBLICATIONChapter:COORDINATE GEOMETRYExercise:STANDARD LEVEL
Explore 46 Videos
- AVERAGESBook:DISHA PUBLICATIONChapter:AVERAGESExercise:Test Yourself
Explore 15 Videos
- FUNCTIONSBook:DISHA PUBLICATIONChapter:FUNCTIONSExercise:Test Yourself
Explore 15 Videos
Similar Questions
Knowledge Check
The area of the figure formed by the lines ax+by+c=0,ax−by+c=0,ax+by−c=0 and ax−by−c=0 is
Ac2abB2c2abCc22abDc24abWhat is the equation of the ellipse whose vertices are (±5,0) and foci are at (±,4,0)?
Ax225+y29=1Bx216+y29=1Cx225+y216=1Dx29+y225=1At what time are the hands of clock together between 7 pm and 8 pm?
A7:45:54B7:36:27C7:37:49D7:38:18
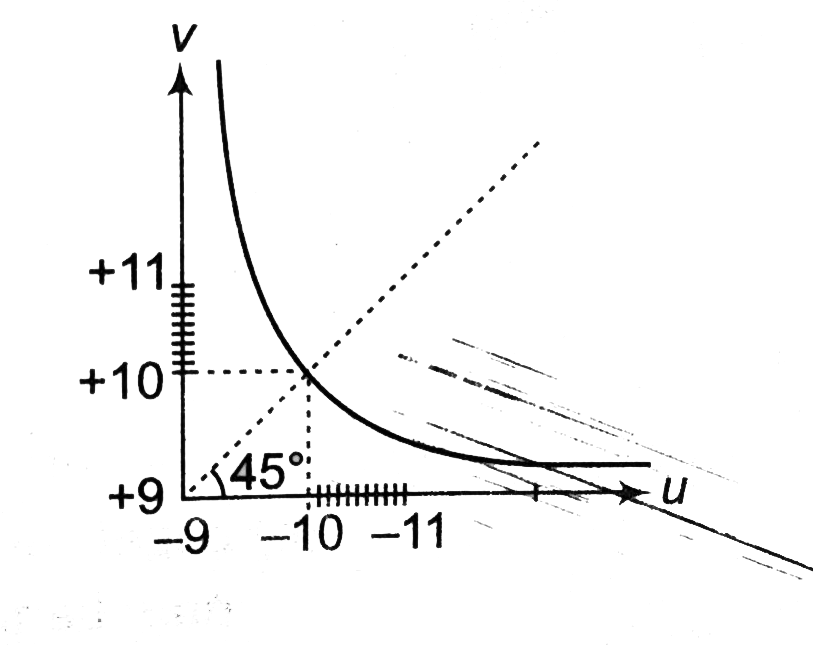
The graph between object distance u and image distancev for a lens is given below. The focal length of the lens is.
(a) 5±0.1
(b) 5±0.05
( c) 0.5±0.1
(d) 0.5±0.05.
 .
.
View SolutionThe length and the width of a rectangular plate are (16.30±0.05)m and (13.80±0.05)m, respectively. Calculate the area of the plate and also find the uncertainty in the area.
View SolutionA clock is displaying correct time at 9am on Monday. If the clock loses 12 minutes in 24 hours, then the actual time when the clock indicates 8:30 pm on Wednesday of the same week is (a) 8 pm (b) 7 pm (c) 9 pm (d) 8:59 :45 pm
View SolutionFind the equation of the ellipse the ends of whose major and minor axes are (±4,0)and(0,±3) respectively.
View SolutionAt what time between 7 o clock and 8 o clock will the hands of a clock be in the same straight line but not together
View Solution