Using Gauss's theorem derive an expression for electric field intensity at a point due to an infinitely long straight uniformly charged wire.
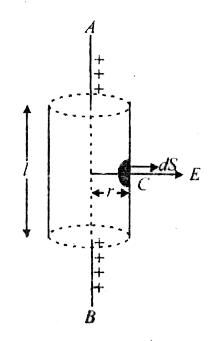
Consider an infinitely long line of charge having a uniform linear charge density λ placed along the axis of cylinder. The cylindrical surface can be treated as the Gaussian surface for the line charges.
Let l be the length and r be the radius of the cylinder. If E is the electric field acting at point C, then electric fluxΦ=E×2πrl curved surface area of the cylinder
or =E×2πrl ........(i) From Gauss.s theorem
Φ=qvatrε0
But q=λl
∴ Φ=λlɛ0
From equation (i) and (ii), E×2πrl=λlɛ0
E=l2πɛ0.λr
Similar Questions
Derive an expression for electric field intensity at a point due to point charge.
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View SolutionUsing Gauss’ law, derive an expression for the electric field at a point near an infinitely long straight uniformly charged wire.
View Solution(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
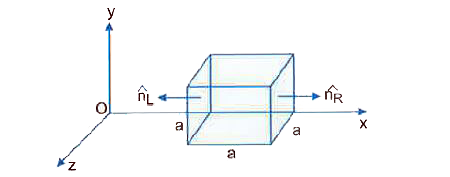
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
View SolutionAnswer the following:
State Gauss' law in electrostatics. Derive an expression for the electric field due to an infinitely long straight uniformly charged wire.
View SolutionApply Gauss's theorem to find an expression for the electric field intensity at a point due to a point charge.
View SolutionDetermine electric field intensity near an infinitely long straight uniformly charge wire.
Or.
Using Gauss' law expression for electric field intensity at a point situated at a distance 'r' from an infinitely long, uniformly charged straight wire.
View SolutionDerive an expression for the electric field intensity at a point outside an infinitely long charged cylindrical conductor.
View SolutionState Gauss's theorem in electrostatiics. State the expression for electric field intensity at a point outside an infinitely long charged conducting cylinder.
View Solution
