Using Gauss's theorem derive an expression for electric field intensity at a point due to an infinite plane sheet of charge.
Or
What is Gauss's law in electrostatics? Using it, obtain an expression for electric field due to uniformly charged thin infinite plane sheet. What would happen, if sheet is thick?

Text Solution

Verified by Experts

Consider a thin infinite plane sheet of charge of surface charge density $σ$ , where $σ = \frac{q}{S}$ . We have to calculate $\to E (P)$ at a distance r from the sheet. Let us take a cylinder of cross-sectional area ds around P of length 2r, piercing through the sheet.

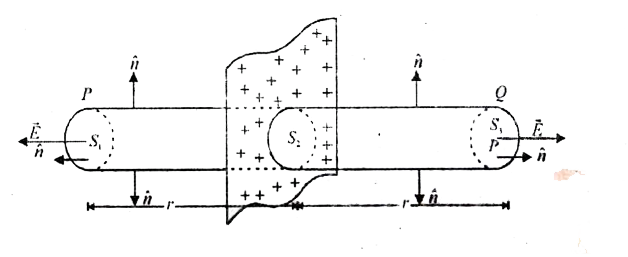
From Gauss.s Law
$Φ_{E} = \int S \to E . - \to d S = \frac{q}{ɛ_{0}}$
Split S into three parts
$\Rightarrow \int S_{2} \to E . - \to d S + \int S_{2} \to E . - \to d S + \int S_{2} \to E . - \to d S = \frac{q}{ɛ_{0}}$
$\Rightarrow \int S_{1} E d S {cos 0}^{\circ} + \int S_{1} E d S {cos 0}^{\circ} + \int S_{1} E d S {cos 0}^{\circ}$
$\int S_{1} E d S + 0 + \int S_{1} E d S = \frac{q}{ɛ_{0}} \Rightarrow E S + E S = \frac{q}{ɛ_{0}} \Rightarrow 2 E S = \frac{q}{ɛ_{0}}$
$B u t q = σ S \Rightarrow 2 E S = \frac{σ S}{ɛ_{0}} or E = \frac{σ}{2 ɛ_{0}}$
In the case, electric field intensity is independent of r. Also, if the sheet carries positive charge, $\to E$ is directed away from the sheet and vice-versa.
Expression for electric field when sheet is thick:
In case of a sheet, with finite thickness, both sides of the sheet are to be considered.
$∴$ from equation (i), we get
$\oint \to E . - \to d S = \frac{2 σ S}{ɛ_{0}}$
$or 2 E S = \frac{2 σ S}{ɛ}$
$or E = \frac{σ}{ɛ_{0}}$
$or E = \frac{σ}{ɛ_{0}} ... . . (v)$

|

Class 12 PHYSICS ELECTROSTATICS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile