Obtain the expression for electric field due to an charged infinite plane sheet . Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Electric field due to charged infinite plane sheet : Consider an infinite plane sheet of charge with uniform surface charge density $σ$ . Let P be a point at a distance of r from the sheet . Since the plane is infinitely large the electric field should be same at all points equidistant from the same at all points equidistant from the plane and radially directed at all points . A cylindrical shaped Gaussian surface of length 2r and area A of the flat surfaces is chosen such that the infinite plane sheet passes perpendicularly through the middle part of the Gaussian surface. Applying Gauss law for this cylindrical surface

$Φ_{E} = \oint \vec{E} . d \vec{A}$
$Φ_{E} = \int_{Curved surface} \vec{E} . d \vec{A} + \int_{P} \vec{E} . d \vec{A} + \int_{P} \vec{E} . d \vec{A} = \frac{Q_{encl}}{ε_{0}}$
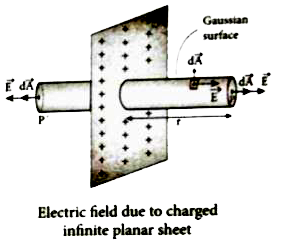
The electric field is perpendicular to the are a element at all point on the curved surface and is parallel to the surface areas at P and P . Then , $Φ_{E} = \int_{P} E d A + \int_{P} E d A = \frac{Q_{encl}}{ε_{0}}$
Since the magnitude of the electric field at these equal surface is uniform E is taken out of the integration and $Q_{encl}$ is given by $Q_{encl} = σ$ A we get
$2 E \int_{P} d A = \frac{σ A}{ε_{0}}$
The total are of surface either at P or P $\int_{P} d A = A$
Hence 2 E A = $\frac{σ A}{ε_{0}}$ or $E = \frac{σ}{2 ε_{0}}$
Hence $2 E A = \frac{σ A}{ε_{0}}$ or $E = \frac{σ}{2 ε_{0}}$
In vector form $E = \frac{σ}{2 ε_{0}} \hat{n}$
Here $\hat{n}$ is the outward unit vector normal to the plane . Note that the electric field due to an infinite plane sheet of charge depends on the surface charge density and is independent of the distance r .
The electric field will be the same at any point farther away from the charged plane . Equation ( 4) implies that if $σ > 0$ the electric field at any point P is outward perpendicular $\hat{n}$ to the plane and if $σ < 0$ the electric field points inward perpendicularly $(- \hat{n})$ to the plane . For a finite charged plane sheet equation (4) is approximately true only in the middle region of the plane and at points far away from ends .

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

FULL MARKS-ELECTROSTATICS -Textual Evaluation Solved ( III. Long Answer Questions: )

Home
Ask Doubt
Profile