A rectangular park 60 metre long and 40 mete wide has concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109metre2 then the width of the road is
3 metre
5 metre
6 metre
2 metre
The correct Answer is:A
To solve the problem, we need to find the width of the concrete road running through the middle of the rectangular park.
1. Calculate the Area of the Park:
The area of a rectangle is given by the formula:
Area=Length×Width
For the park:
Area of the park=60m×40m=2400m2
2. Determine the Area of the Lawn:
We are given that the area of the lawn is 2109m2.
3. Calculate the Area of the Road:
The area of the road can be found by subtracting the area of the lawn from the area of the park:
Area of the road=Area of the park−Area of the lawn
Area of the road=2400m2−2109m2=291m2
4. Set Up the Equation for the Width of the Road:
Let the width of the road be xm. The road runs through the middle of the park, creating a crossroad. The dimensions of the road will be:
- Length of the road = 60 m (the length of the park)
- Width of the road = xm (the width we need to find)
The area of the road can be expressed as:
Area of the road=Length×Width+Width×Length
Since there are two roads (one horizontal and one vertical), the area becomes:
Area of the road=60x+40x−x2
Here, x2 is subtracted because the intersection of the two roads has been counted twice.
5. Set Up the Equation:
Now we equate the area of the road to the calculated area:
60x+40x−x2=291
Simplifying this gives:
100x−x2=291
Rearranging gives:
x2−100x+291=0
6. Solve the Quadratic Equation:
We can use the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−100,c=291.
x=100±√(−100)2−4⋅1⋅2912⋅1
x=100±√10000−11642
x=100±√88362
x=100±942
This gives us two potential solutions:
x=1942=97(not possible, as it exceeds the park's width)
x=62=3
7. Conclusion:
The width of the road is 3m.
The area of a rectangle is given by the formula:
Area=Length×Width
For the park:
Area of the park=60m×40m=2400m2
We are given that the area of the lawn is 2109m2.
The area of the road can be found by subtracting the area of the lawn from the area of the park:
Area of the road=Area of the park−Area of the lawn
Area of the road=2400m2−2109m2=291m2
Let the width of the road be xm. The road runs through the middle of the park, creating a crossroad. The dimensions of the road will be:
- Length of the road = 60 m (the length of the park)
- Width of the road = xm (the width we need to find)
Area of the road=Length×Width+Width×Length
Since there are two roads (one horizontal and one vertical), the area becomes:
Area of the road=60x+40x−x2
Here, x2 is subtracted because the intersection of the two roads has been counted twice.
Now we equate the area of the road to the calculated area:
60x+40x−x2=291
Simplifying this gives:
100x−x2=291
Rearranging gives:
x2−100x+291=0
We can use the quadratic formula x=−b±√b2−4ac2a:
Here, a=1,b=−100,c=291.
x=100±√(−100)2−4⋅1⋅2912⋅1
x=100±√10000−11642
x=100±√88362
x=100±942
This gives us two potential solutions:
x=1942=97(not possible, as it exceeds the park's width)
x=62=3
The width of the road is 3m.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - III21videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV169videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
A rectangular park 60 m long and 40 m wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 sq. m, then what is the width of the road? (a) 2.91m (b) 3m (c) 5.82m (d) None of these
View SolutionA rectangular park is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.
View Solution
Knowledge Check
- Question 1 - Select One
A rectangle park is 45 m long and 30 m wide. A path 2.5 m wide is constructed outside the park. Find the area of the path.
A200m2B300m2C400m2D375m2 - Question 2 - Select One
A rectangular park is 100 m long and 60 m wide. There is a path 2 m wide out side the park. Find the area of the path?
A324m2B656m2C675m2D780m2
A rectangular park is 2034 m long and 1512 m wide. What is the area of the park?
View SolutionA rectangular lawn is 30 m by 20 m. It has two roads each 2 m wide running in the middle of it one parallel to the length and the other parallel to the breadth. Find the area of the roads.
View SolutionA rectangular grass plot 80m×60m has two roads, each 10 m wide, running in the middle of it, one parallel to length and the other parallel to breadth.Find the area of the roads.
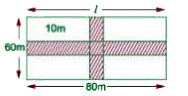 View Solution
View SolutionA rectangular lawn is 60 m by 40 m and has two roads. each 5 m wide running in the middle of it, one parallel to its length and the other parallel to the breadth, as shown in the figure. Find the cost of constructing the roads at Rs. 80 per m2.
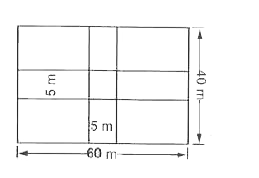 View Solution
View SolutionA rectangular park 35 m long and 18 m wide is to be covered with grass, leaving 2.5 m uncovered all around it .Find the area to be laid with grass.
View SolutionA park is 1500 metres long and 750 metres wide. A cyclist has to take four rounds of this park.How much time will he take at the speed of 4.5 km/hr?
View Solution

