Two cubes of sides 6 cm each are kept side by side to form a rectangular parallelopiped. The area (in sq. cm) of the whole suface of the rectangular parallelopiped is
432
360
396
340
The correct Answer is:B
To find the surface area of the rectangular parallelepiped formed by placing two cubes of side 6 cm side by side, we will follow these steps:
Step 1: Understand the dimensions of the rectangular parallelepiped
When two cubes of side 6 cm are placed side by side, the dimensions of the rectangular parallelepiped will be:
- Length (l) = 2 × side of the cube = 2 × 6 cm = 12 cm
- Width (w) = side of the cube = 6 cm
- Height (h) = side of the cube = 6 cm
Step 2: Use the formula for the surface area of a rectangular parallelepiped
The formula for the surface area (SA) of a rectangular parallelepiped is given by:
SA=2(lw+lh+wh)
Step 3: Substitute the dimensions into the formula
Now, substituting the values we found:
- l = 12 cm
- w = 6 cm
- h = 6 cm
We calculate:
SA=2(12×6+12×6+6×6)
Step 4: Calculate each term
Calculating each term:
- lw=12×6=72
- lh=12×6=72
- wh=6×6=36
Step 5: Add the terms together
Now, add these values:
SA=2(72+72+36)=2(180)
Step 6: Final calculation
Now, multiply by 2:
SA=2×180=360 sq. cm
Conclusion
The area of the whole surface of the rectangular parallelepiped is 360 sq. cm.
---
When two cubes of side 6 cm are placed side by side, the dimensions of the rectangular parallelepiped will be:
- Length (l) = 2 × side of the cube = 2 × 6 cm = 12 cm
- Width (w) = side of the cube = 6 cm
- Height (h) = side of the cube = 6 cm
The formula for the surface area (SA) of a rectangular parallelepiped is given by:
SA=2(lw+lh+wh)
Now, substituting the values we found:
- l = 12 cm
- w = 6 cm
- h = 6 cm
SA=2(12×6+12×6+6×6)
Calculating each term:
- lw=12×6=72
- lh=12×6=72
- wh=6×6=36
Now, add these values:
SA=2(72+72+36)=2(180)
Now, multiply by 2:
SA=2×180=360 sq. cm
The area of the whole surface of the rectangular parallelepiped is 360 sq. cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE VI47videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
Knowledge Check
- Question 1 - Select One
The ratio of the length and breadth of a rectangular parallelopiped is 5:3. and its height is 6 cm. If the total surface area of the parallelopiped be 558 sq. cm, then its length in dm is
A9B1.5C10D15 - Question 2 - Select One
In the figure, side of each square is 1 cm. The area, in sq cm of the shaded part
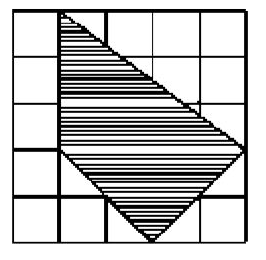 A8B9C10D11
A8B9C10D11 - Question 3 - Select One
If two adjacent sides of a rectangular parallelopiped are 1 cm and 2 cm and the total surface area of the parallelopiped is 22 square cm, then the diagonal of the parallelopied is
A√10cmB2√3cmC√14cmD4 cm
Three cubes of sides 1 cm, 6 cm and 8 cm are melted to form a new cube. Find half of the surface area of the new cube.
View SolutionThree cubes of sides 6 cm, 8 cm and 1 cm are melted to form a new cube. The surface area of the new cube is
View SolutionWhat is the area (in sq cm.) of the regular hexagon side 14 cm ?
View SolutionIn the figure, side of each square is 1 cm. The area, in sq cm of the shaded part
 View Solution
View SolutionThe dimensions of a rectangular parallelepiped are in the ratio 2:2:1 and the area of its whole surface is 144 sq. cm. Its volume is
View Solution

