The base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB=90∘. If the volume of the prism be 2070cm3, then the area of the lateral surface is
720cm2
810cm2
1260cm2
2070cm2
The correct Answer is:A
To solve the problem of finding the lateral surface area of a right prism with a quadrilateral base ABCD, we will follow these steps:
Step 1: Identify the dimensions of the quadrilateral
Given:
- AB = 9 cm
- BC = 14 cm
- CD = 13 cm
- DA = 12 cm
- Angle DAB = 90°
Step 2: Divide the quadrilateral into two triangles
We can divide quadrilateral ABCD into two triangles: Triangle ABD and Triangle BCD.
Step 3: Calculate the area of Triangle ABD
Triangle ABD is a right triangle (since angle DAB = 90°). We can use the formula for the area of a triangle:
Area=12×base×height
Here, AB is the base and AD is the height.
Area of △ABD=12×AB×AD=12×9×12=54cm2
Step 4: Calculate the length of diagonal BD using Pythagorean theorem
Using the Pythagorean theorem in triangle ABD:
BD=√AB2+AD2=√92+122=√81+144=√225=15cm
Step 5: Calculate the area of Triangle BCD using Heron's formula
First, calculate the semi-perimeter (s) of triangle BCD:
s=BC+CD+BD2=14+13+152=21cm
Now, apply Heron's formula:
Area=√s(s−BC)(s−CD)(s−BD)
Area of △BCD=√21(21−14)(21−13)(21−15)
=√21×7×8×6
Calculating this gives:
=√21×336=√7056=84cm2
Step 6: Calculate the total area of the base (quadrilateral ABCD)
Area of ABCD=Area of △ABD+Area of △BCD
=54+84=138cm2
Step 7: Find the height of the prism
Using the formula for volume:
Volume=Area of base×Height
Given that the volume is 2070 cm³:
2070=138×Height
Height=2070138=15cm
Step 8: Calculate the perimeter of the base
Perimeter=AB+BC+CD+DA=9+14+13+12=48cm
Step 9: Calculate the lateral surface area
The lateral surface area (LSA) of the prism is given by:
LSA=Perimeter×Height
LSA=48×15=720cm2
Final Answer
The area of the lateral surface is 720 cm².
---
Given:
- AB = 9 cm
- BC = 14 cm
- CD = 13 cm
- DA = 12 cm
- Angle DAB = 90°
We can divide quadrilateral ABCD into two triangles: Triangle ABD and Triangle BCD.
Triangle ABD is a right triangle (since angle DAB = 90°). We can use the formula for the area of a triangle:
Area=12×base×height
Here, AB is the base and AD is the height.
Area of △ABD=12×AB×AD=12×9×12=54cm2
Using the Pythagorean theorem in triangle ABD:
BD=√AB2+AD2=√92+122=√81+144=√225=15cm
First, calculate the semi-perimeter (s) of triangle BCD:
s=BC+CD+BD2=14+13+152=21cm
Area=√s(s−BC)(s−CD)(s−BD)
Area of △BCD=√21(21−14)(21−13)(21−15)
=√21×7×8×6
Calculating this gives:
=√21×336=√7056=84cm2
Area of ABCD=Area of △ABD+Area of △BCD
=54+84=138cm2
Using the formula for volume:
Volume=Area of base×Height
Given that the volume is 2070 cm³:
2070=138×Height
Height=2070138=15cm
Perimeter=AB+BC+CD+DA=9+14+13+12=48cm
The lateral surface area (LSA) of the prism is given by:
LSA=Perimeter×Height
LSA=48×15=720cm2
The area of the lateral surface is 720 cm².
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - Test Yourself28videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE VI47videos
MENSURATION
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
- BOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI15videos
MISCELLANEOUS
Similar Questions
Knowledge Check
- Question 1 - Select One
The base of a right prism is a quadrilateral ABCD. Given that AB = 9 cm, BC = 14 cm, CD = 13 cm, DA = 12 cm and ∠DAB=90∘. If the volume of the prism be 2070cm3, then the area of the lateral surface is
A720 वर्ग सेमीB810 वर्ग सेमीC1260 वर्ग सेमीD2070 वर्ग सेमी - Question 2 - Select One
A park is in the shape of quadrilateral ABCD in which AB=9cm,BC=12cm,CD=5cm,AD=8cm and ∠C=90∘. Find the area of the park.
A65.4cm2B69.4cm2C66.4cm2D68.4cm2 - Question 3 - Select One
All sides of a quadrilateral ABCD touch a circle. If AB=6cm,BC=7.5cm,CD=3cm, then DA is
A3.5 cmB4.5 cmC2.5 cmD1.5 cm
In a quadrilateral ABCD , AB = 5 cm , BC = 37 cm , CD = 35 cm , BD = 12 cm , and AD = 13 cm . Find its area .
View SolutionIn a quadrilateral ABCD, AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm and diagonal AC = 30 cm. Find the area of the quadrilateral.
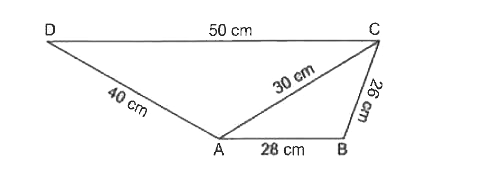 View Solution
View SolutionConstruct a quadrilateral ABCD in which AB=3.8cm, BC=5cm,CD=5cm, DA=5.5cm and AC=8cm.
View SolutionA circle is inscribed in the quadrilateral ABCD. Given BC= 38 cm . BQ= 27 cm , CD = 25 cm and ∠ADC=90∘ find the radius of the circle .
View SolutionFind the area of the quadrilateral ABCD, in which AB=7cm, BC=6cm, CD=12 cm, DA=15cm and AC=9 cm.
View Solution

