In ΔPQR, PQ = 4 cm, QR = 3 cm and RP = 3.5 cm, ΔDEF is similar to ΔPQR. If EF = 9 cm then perimeter of ΔDEF is -
10.5 cm
21 cm
31.5 cm
Cannot be determined
The correct Answer is:C
To find the perimeter of triangle DEF, we will use the properties of similar triangles. Here are the steps to solve the problem:
Step 1: Find the perimeter of triangle PQR
The perimeter of triangle PQR is the sum of its sides. Given:
- PQ = 4 cm
- QR = 3 cm
- RP = 3.5 cm
Calculation:
Perimeter of ΔPQR=PQ+QR+RP=4+3+3.5=10.5 cm
Step 2: Set up the ratio of the perimeters
Since triangles DEF and PQR are similar, the ratio of their perimeters is equal to the ratio of their corresponding sides. We can express this as:
Perimeter of ΔDEFPerimeter of ΔPQR=EFQR
Step 3: Substitute the known values
We know:
- EF = 9 cm
- QR = 3 cm
- Perimeter of PQR = 10.5 cm
Substituting these values into the ratio gives:
Perimeter of ΔDEF10.5=93
Step 4: Simplify the ratio
Simplifying the right side:
93=3
Step 5: Solve for the perimeter of triangle DEF
Now we can solve for the perimeter of triangle DEF:
Perimeter of ΔDEF=10.5×3=31.5 cm
Final Answer:
The perimeter of triangle DEF is 31.5 cm.
---
The perimeter of triangle PQR is the sum of its sides. Given:
- PQ = 4 cm
- QR = 3 cm
- RP = 3.5 cm
Perimeter of ΔPQR=PQ+QR+RP=4+3+3.5=10.5 cm
Since triangles DEF and PQR are similar, the ratio of their perimeters is equal to the ratio of their corresponding sides. We can express this as:
Perimeter of ΔDEFPerimeter of ΔPQR=EFQR
We know:
- EF = 9 cm
- QR = 3 cm
- Perimeter of PQR = 10.5 cm
Perimeter of ΔDEF10.5=93
Simplifying the right side:
93=3
Now we can solve for the perimeter of triangle DEF:
Perimeter of ΔDEF=10.5×3=31.5 cm
The perimeter of triangle DEF is 31.5 cm.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B28videos
ALGEBRAIC IDENTITIES
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B27videos
CIRCLE AND ITS TANGENT LINES
Similar Questions
Knowledge Check
- Question 1 - Select One
In Δ PQR, PQ = 4 cm, QR = 3 cm, and RP = 3.5 cm. Δ DEF is similar to Δ PQR. If EF = 9 cm, then what is the perimeter of Δ DEF ?
A10.5 cmB21 cmC31.5 cmDCannot be determined as data is insufficient - Question 2 - Select One
ΔABC is such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm. If ΔABC~ΔDEF and EF= 4 cm, then perimeter of ΔDEF is :
A7.5 cmB15 cmC22.5 cmD30 cm - Question 3 - Select One
ΔABC−ΔRQP and PQ = 10 cm, QR = 12 cm and RP = 16 cm. If ar (ΔPQR) : ar (ΔABC)=94 then BC is equal to:
A6 cmB203 cmC8 cmD223cm
ΔABC~ΔPQR. If AB= 4cm, BC=3cm, CA=7cm and PR=2cm, then the perimeter of ΔPQR is
View SolutionΔABC~ΔDEF such that AB = 9.1 cm and DE =6.5 cm. If the perimeter of ΔDEF is 25 cm, what is the perimeter of ΔABC?
View SolutionIn given figure , OP = 5 cm and OR =12 cm and QR = 85 cm find the area of ΔPQR .
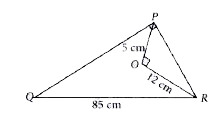 View Solution
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
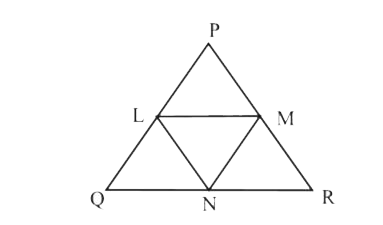 View Solution
View SolutionIn ΔPQR,∠PQR=90∘,PQ=5cmandQR=12cm. What is the radius (in cm) of the circum-circle of ΔPQR?
View Solution

