At the foot of a mountain the elevation of its summit is 45∘. After ascending 2000 meter towards the mountain upon an incline of 30∘, the elevation changes to 60∘. What is the height of the mountain.
2000(√3−1) meter
1000(√3−1) meter
2000(√3+1) meter
1000(√3+1) meter
The correct Answer is:B
To solve the problem step by step, we will analyze the situation using trigonometry and the given angles of elevation.
Step 1: Understand the problem
We have a mountain with an angle of elevation of 45 degrees at its base. After ascending 2000 meters towards the mountain at an incline of 30 degrees, the angle of elevation changes to 60 degrees. We need to find the height of the mountain.
Step 2: Set up the scenario
Let:
- h = height of the mountain
- A = point at the foot of the mountain
- B = point after ascending 2000 meters
- C = summit of the mountain
Step 3: Use the first angle of elevation (45 degrees)
From point A, the angle of elevation to the summit C is 45 degrees. Using the tangent function:
tan(45∘)=hd
where d is the horizontal distance from point A to point C.
Since tan(45∘)=1:
h=d(1)
Step 4: Use the second angle of elevation (60 degrees)
After ascending 2000 meters towards the mountain at an incline of 30 degrees, we need to find the new horizontal distance from point B to point C.
The horizontal distance d′ from point B to point C can be calculated as follows:
- The vertical rise from point B due to the incline of 30 degrees is:
Vertical rise=2000sin(30∘)=2000×12=1000 meters
- The horizontal distance covered from point B is:
Horizontal distance=2000cos(30∘)=2000×√32=1000√3 meters
Thus, the new horizontal distance d′ from point B to point C is:
d′=d−1000√3(2)
Using the angle of elevation of 60 degrees from point B:
tan(60∘)=h−1000d′
Since tan(60∘)=√3:
√3=h−1000d−1000√3(3)
Step 5: Substitute equation (1) into equation (3)
From equation (1), we know h=d. Substituting h in equation (3):
√3=d−1000d−1000√3
Step 6: Cross-multiply and solve for d
Cross-multiplying gives:
√3(d−1000√3)=d−1000
Expanding and rearranging:
√3d−3000=d−1000
√3d−d=3000−1000
(√3−1)d=2000
d=2000√3−1(4)
Step 7: Substitute d back to find h
Using equation (1):
h=d=2000√3−1
Step 8: Rationalize the denominator
To simplify:
h=2000(√3+1)(√3−1)(√3+1)=2000(√3+1)3−1=1000(√3+1)
Final Answer
The height of the mountain is:
h=1000(√3+1) meters
We have a mountain with an angle of elevation of 45 degrees at its base. After ascending 2000 meters towards the mountain at an incline of 30 degrees, the angle of elevation changes to 60 degrees. We need to find the height of the mountain.
Let:
- h = height of the mountain
- A = point at the foot of the mountain
- B = point after ascending 2000 meters
- C = summit of the mountain
From point A, the angle of elevation to the summit C is 45 degrees. Using the tangent function:
tan(45∘)=hd
where d is the horizontal distance from point A to point C.
h=d(1)
After ascending 2000 meters towards the mountain at an incline of 30 degrees, we need to find the new horizontal distance from point B to point C.
- The vertical rise from point B due to the incline of 30 degrees is:
Vertical rise=2000sin(30∘)=2000×12=1000 meters
- The horizontal distance covered from point B is:
Horizontal distance=2000cos(30∘)=2000×√32=1000√3 meters
d′=d−1000√3(2)
tan(60∘)=h−1000d′
Since tan(60∘)=√3:
√3=h−1000d−1000√3(3)
From equation (1), we know h=d. Substituting h in equation (3):
√3=d−1000d−1000√3
Cross-multiplying gives:
√3(d−1000√3)=d−1000
Expanding and rearranging:
√3d−3000=d−1000
√3d−d=3000−1000
(√3−1)d=2000
d=2000√3−1(4)
Using equation (1):
h=d=2000√3−1
To simplify:
h=2000(√3+1)(√3−1)(√3+1)=2000(√3+1)3−1=1000(√3+1)
The height of the mountain is:
h=1000(√3+1) meters
Topper's Solved these Questions
- HEIGHT AND DISTANCEBOOK - LUCENT PUBLICATIONCHAPTER - HEIGHT AND DISTANCEEXERCISE - EXERCISE-12B
14 Videos
- HEIGHT AND DISTANCEBOOK - LUCENT PUBLICATIONCHAPTER - HEIGHT AND DISTANCEEXERCISE - EXERCISE-12B
14 Videos
- GRAPHICAL SOLUTION OF LINEAR EQUATION BOOK - LUCENT PUBLICATIONCHAPTER - GRAPHICAL SOLUTION OF LINEAR EQUATION EXERCISE - EXERCISE-3B
8 Videos
- INDICES AND SURDS BOOK - LUCENT PUBLICATIONCHAPTER - INDICES AND SURDS EXERCISE - Exercise - 2B
14 Videos
Similar Questions
At the foot of a mountain the elevation of its summit is 45∘. After ascending 600 meter towards the mountain, upon an incline of 30∘, the elevation changes to 60∘. Find the height of the mountain.
View SolutionAt the foot of a mountain, the elevation of its summit is 45∘. After ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. find the height of the mountain.
View Solution
Knowledge Check
At the foot of a mountain, the elevation of its summit is 45∘. After ascending 2 km towards the mountain upon an incline of 30∘, the elevation changes to 60∘. The height of the mountain is
A(√3−1)kmB(√3+1)kmC(√3−2)kmD(√3−2)kmAt the foot of the mountain the elevation of its summit is 45∘, after ascending 100 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘. The height of the mountain is
A√3+12mB√3−13 mC√3+12√3 mDnone of theseAt the foot of the mountain, the elevation of its summit is 45∘ , after ascending 1000 m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ . The height of the mountain is
A√3+12mB√3−12mC√3+12√3Dnone of these
At the foot of a mountain the elevation of its summit is 45∘, after ascending 1000m towards the mountain up a slope of 30∘ inclination, the elevation is found to be 60∘ Find the height of the mountain.
View SolutionAt the foot of a mountain the elevation of its summit is 450; after ascending 1000 m towards the mountain up a slope of 300 inclination, the elevation is fund to be 600 . Find the height of the mountain.
View SolutionAt the foot of a mountain, the angle of elevation of its summit is 45∘. After ascending 1 km towards the mountain up an incline of 30∘, the elevatioon changes to 60∘ (as shown in the given figure). Find the height of the mountain. [Given: √3=1.73.]
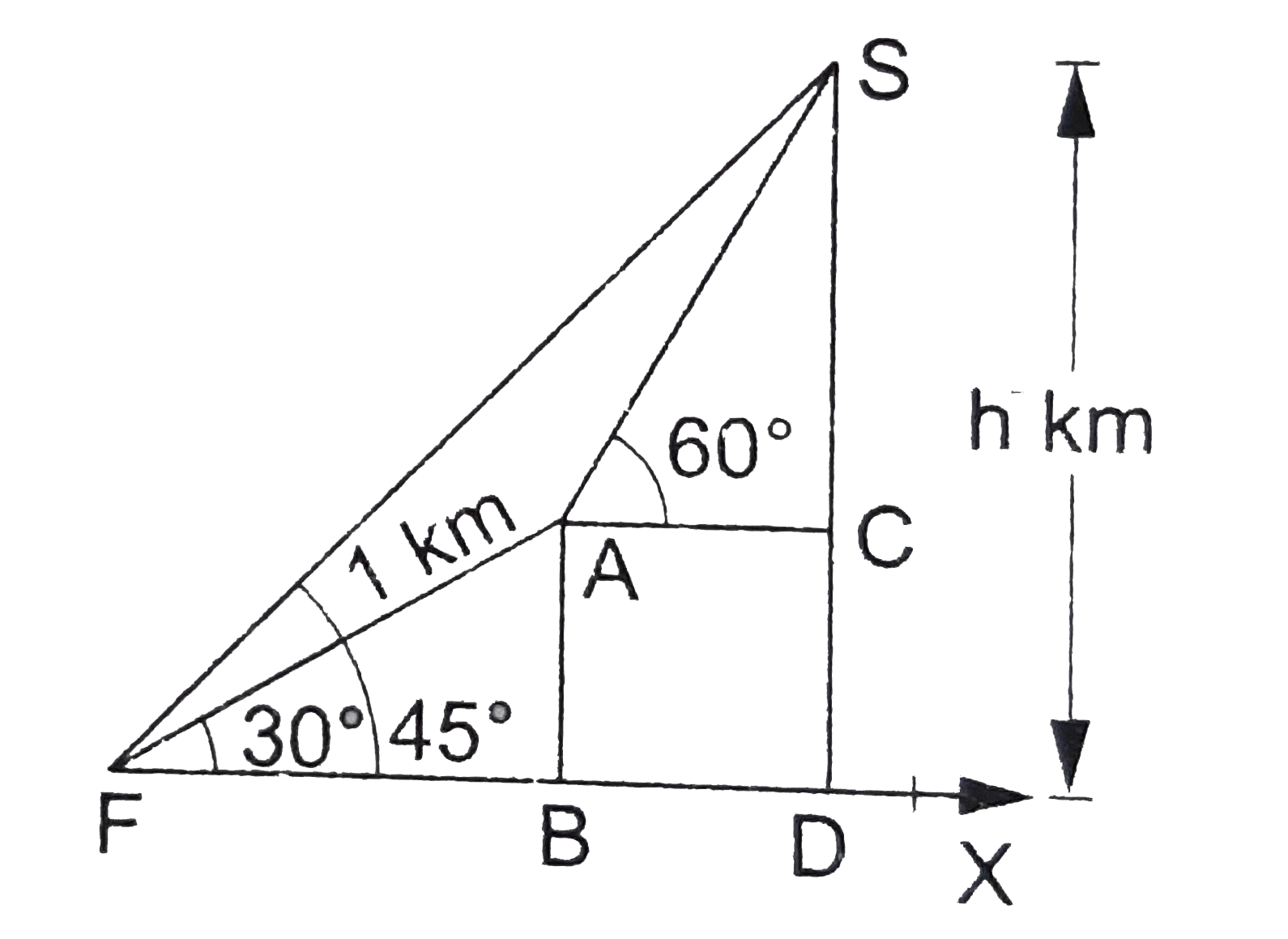
View SolutionAt the foot of a mountain the elevation of it's peak is found to be(π4) ,after ascending 'h' meters toward the mountain up a slope of π6 inclination,the elevation is found to be π3 .Height of the mountain is
View SolutionFrom a point on the ground, the angle of elevation of a summit is found to be 45∘. After walking 150mt towards the mountain, the angle of elevation of the summit is found to be 60∘. The height of the mountain is:
View Solution
