Find an expression for magnetic flux density at the centre of a circular coil carrying current.
Let us consider a circular loop of radius a with centre C. The plane of the coil be perpendicular to the plane of the paper and current I be flowing in the direction shown. Suppose P is any point on the axis at direction r from the centre.
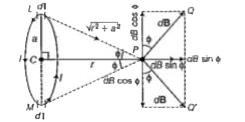
Now, consider a current element I dl on top (L). where current comes out of paper normally, whereas at bottom (M) enters into the plane paper normally.
LP⊥dl
Also, MP⊥dl
LP=MP=√r2+a2
The magnetic field at P due to current element Idl, according to Biot-Savart.s law is given by
dB=μ04π⋅Idlsin90∘(r2+a2)
where, a = radius of circular loop
and r= distance of point P from centre along the axis.
Net magnetic field,
B=∮dBsinϕ=∮μ04π(Idlr2+a2)⋅a√r2+a2
[∴sinϕ=a√r2+a2,inΔPCL]
=μ04πIa(r2+a2)3/2∮dl
B=μ04πIa(r2+a2)3/2(2πa) [∴dl=2πa]
or B=μ0la22(r2+a2)3/2 .......(i)
For N turns, B=μ0NIa22(r2+a2)3/2
The direction is along the axis and away from the loop, current in coil is anti-clockwise. Now putting, r = 0 in Eq. (i) as for centre, we get
B=μ0I2a.
Similar Questions
Knowledge Check
- Question 1 - Select One
The magnetic moment of a circular coil carrying current is
ADirectly proportional to the length of the wire in the coilBInversely proportional to the length of the wire in the coilCDirectly proportional to the square of the length of the wire in the coilDInversely proportional to the square of the length of the wire in the coil - Question 2 - Select One
The magnetic field at the centre of current carrying coil is
Aμ0ni2rBμ02πnirCμ0ni4rDμ0ni
Plot a magnetic field due to a circular coil carrying current and explain the law used to find the direction of magnetic field at the centre of circular coil carrying current.
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionHow will the magnetic field induction at the centre of a circular coil carrying current change, if the current through the coil is doubled and the radius of the coil is halved?
View SolutionHow will the magnetic field induction at the centre of a circular coil carrying current change, if the current through the coil is doubled and the radius of the coil is halved?
View SolutionFind an expression for the magnetic field induction at the centre of a coil bent in the form of a square of side 2a, carrying current I, figure
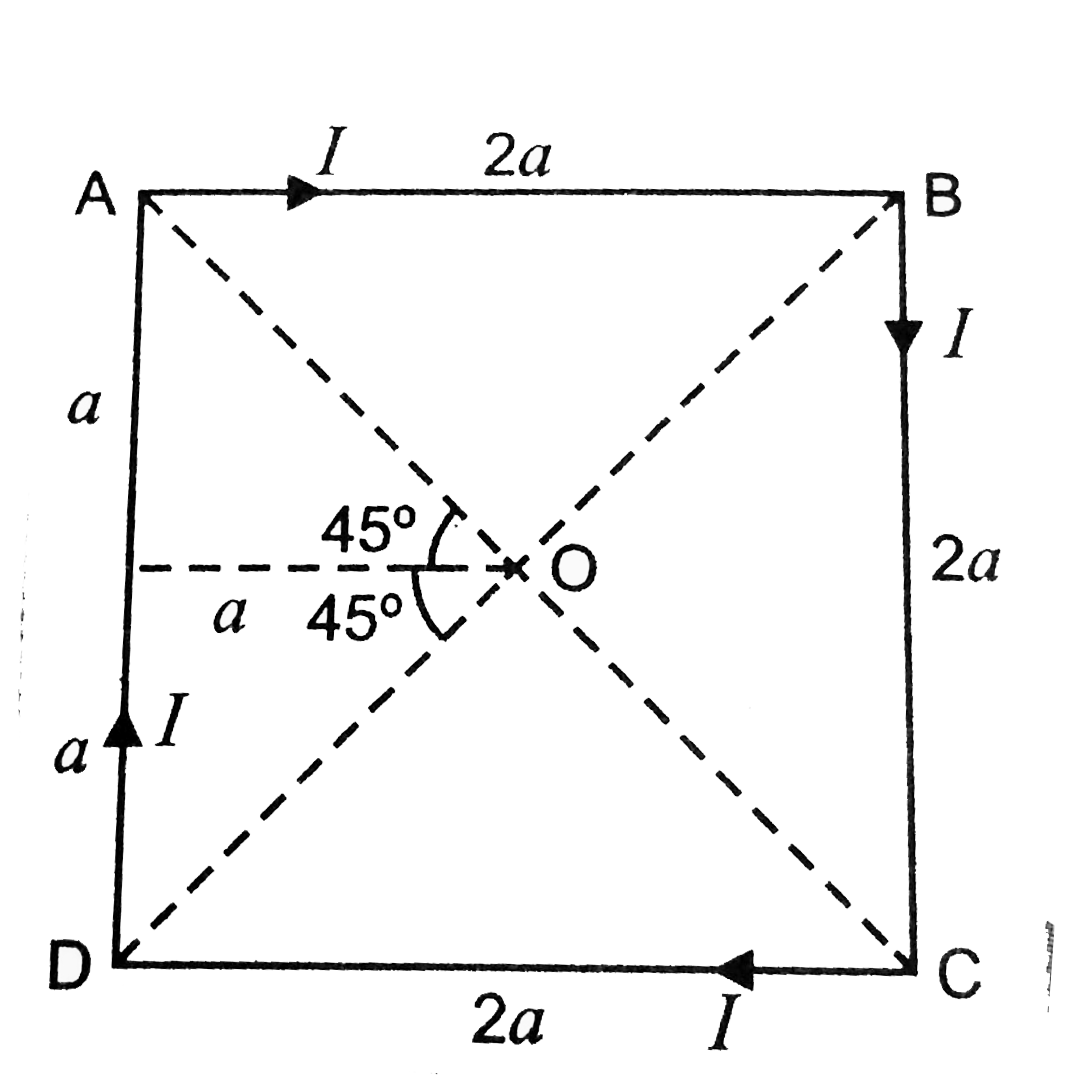 View Solution
View Solution

