The intensity at the central maxima (O) in a Young's double slit experiment is $I_{0}$ . If the distance OP equals to one-third of fringe width of the pattern, show that the intensity at point P would be $I_{0}$ /4

Text Solution

Verified by Experts

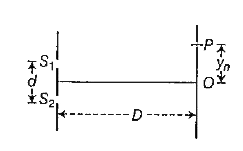
Given distance OP = $y_{n}$
The distance OP equals one - third of fringe width of the pattern
$y_{n} = \frac{β}{3} = \frac{1}{3} (\frac{D λ}{d}) = \frac{D λ}{d} \Rightarrow \frac{{d y}_{n}}{D} = \frac{λ}{3}$
Path difference $S_{2} P - S_{1} P = \frac{{d y}_{n}}{D} = \frac{λ}{3}$
Now for phase difference corresponding to path difference .
Phase difference = $\frac{2 π}{λ} \times$ Path difference
$= \frac{2 π}{λ} \times \frac{λ}{3}$
$∴$ Phase difference = $\frac{2 π}{3}$
If intensity at central fringe is $l_{0}$ then intensity at a point P where phase difference is $ϕ$ is given by
$l = l_{0} {cos}^{2} ϕ$
$\Rightarrow l = l_{0} {(cos \frac{2 π}{3})}^{2} = l_{0} {(- \frac{1}{2})}^{2} = \frac{l_{0}}{4}$

Updated on:21/07/2023