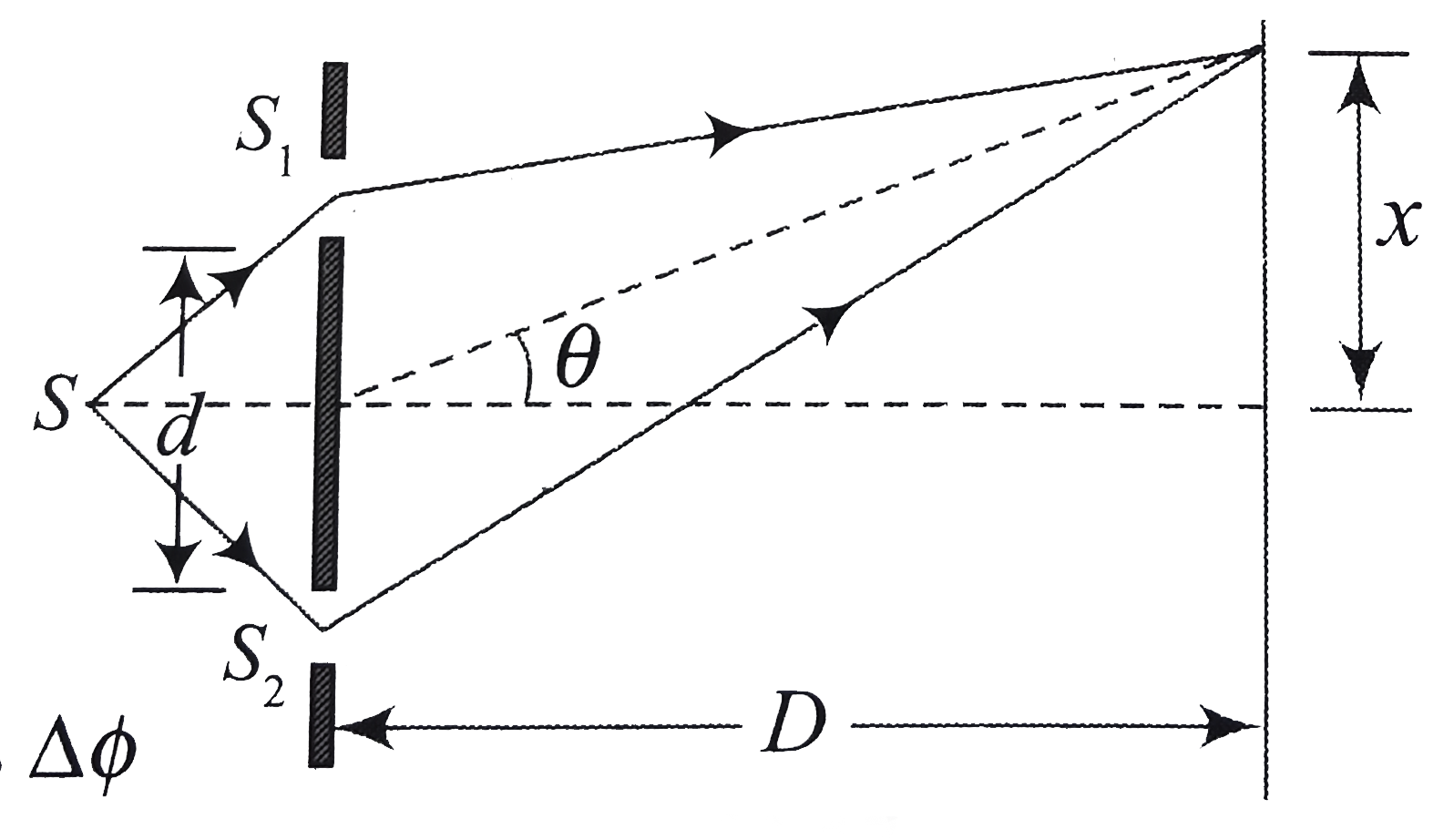
In YDSE, having slits of equal width, let $β$ be the fringe width and $I_{0}$ be the maximum intensity. At a distance x from the central brigth fringe, the intensity will be

A

$I_{0} cos (\frac{x}{β})$

B

$I_{0} {cos}^{2} (\frac{2 π x}{β})$

C

$I_{0} {cos}^{2} (\frac{π x}{β})$

D

$\frac{I_{0}}{4} {cos}^{2} (\frac{π x}{β})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c

At point P, $Δ ϕ = \frac{2 π}{λ} Δ x$ and $Δ x = \frac{d x}{Δ}$
$Δ ϕ = \frac{2 π}{λ} \times \frac{d x}{D} = \frac{2 π x}{β}$
$I_{P} = I_{1} + I_{2} + 2 \sqrt{I_{1} I_{2}} o c s Δ ϕ, I_{1} = I_{2} = I$
$I_{P} = 4 I \frac{{cos}^{2} (Δ d)}{2}$
Given $4 I = I_{0}$
$\Rightarrow I_{1} = I_{2} = \frac{I_{0}}{4}$
$I_{P} = \frac{I_{0}}{2} + \frac{I_{0}}{2} cos Δ ϕ$
$I_{P} = I_{0} {cos}^{2} (\frac{Δ ϕ}{2}) = I_{0} {cos}^{2} (\frac{π x}{β})$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In YDSE of equal width slits, if intensity at the center of screen is $I_{0}$ , then intensity at a distance of $β / 4$ from the central maxima is
A $I_{0}$
B $\frac{I_{0}}{2}$
C $\frac{I_{0}}{4}$
D $\frac{I_{0}}{3}$
Question 2 - Select One
In a double slit experiment ,the separation between the slits is $d = 0.25 c m$ and the distance of the screen $D = 100$ cm from the slits .if the wavelength of light used in $λ = 6000 Å$ and $I_{0}$ is the intensity of the central bright fringe.the intensity at a distance $x = 4 \times 10^{- 5}$ in form the central maximum is-
A $I_{0}$
B $I_{0} / 2$
C $3 I_{0} / 4$
D $I_{0} / 3$
Question 3 - Select One
In YDSE, when separation between two slits is increased, fringe width
Adecreases
Bincreases
Cremains the same
Dnone of these

CENGAGE PHYSICS-WAVE OPTICS-Single Correct

Home
Ask Doubt
Profile