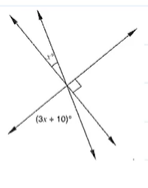
If (7x+5)∘ and (x+5)∘ are complementary angles, then find value of x. Options are (a) 10 (b) 20 (c) 30 (d) 40.
10
20
30
40
To solve the problem, we need to find the value of x given that the angles (7x+5)∘ and (x+5)∘ are complementary. Complementary angles add up to 90∘.
1. Set Up the Equation:
Since the angles are complementary, we can write the equation:
(7x+5)+(x+5)=90
2. Combine Like Terms:
Combine the terms on the left side of the equation:
7x+5+x+5=90
This simplifies to:
8x+10=90
3. Isolate the Variable:
To isolate 8x, subtract 10 from both sides:
8x=90−10
This simplifies to:
8x=80
4. Solve for x:
Now, divide both sides by 8:
x=808
Thus, we find:
x=10
5. Conclusion:
The value of x is 10.
Final Answer:
The correct option is (a) 10.
Since the angles are complementary, we can write the equation:
(7x+5)+(x+5)=90
Combine the terms on the left side of the equation:
7x+5+x+5=90
This simplifies to:
8x+10=90
To isolate 8x, subtract 10 from both sides:
8x=90−10
This simplifies to:
8x=80
Now, divide both sides by 8:
x=808
Thus, we find:
x=10
The value of x is 10.
The correct option is (a) 10.
Similar Questions
Knowledge Check
If the mean of 5, 7, x, 10, 5, and 7 is 7, then find the value of x.
A6B7C8D9
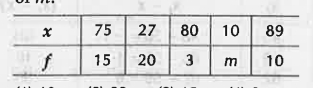
If the mean of the following observation be 56.5, find the value of m. Options are (a) 10 (b) 20 (c) 12 (d) 2.
View SolutionIn Fig.73, the value of x is 20 (b) 30 40 (d) 25
View SolutionIf two complementary angles are (x−3) and (x+7) ,find the angles
View SolutionThe minimum valueof|x-3|+|x-2|+|x-5| is (A) 3 (B) 7 (C) 5 (D) 9
View SolutionThe average of 2, 7, 6 and x is 5 and the average of 18, 1, 6, x and y is 10. What is the value of y ? (a) 5 (b) 10 (c) 20 (d) 30
View SolutionIf the arithmetic mean of 7, 5, 13, x and 9 is 10, then the value of x is 10 (b) 12 (c) 14 (d) 16
View SolutionIf the sum of the binomial coefficients in the expansion of (x+1x)n is 64, then the term independent of x is equal to (A) 10 (B) 20 (C) 30 (D) 40
View Solution