Let PAB be a secant to a circle intersecting at points A and B, and PC is a tangent. Which one of the following is correct?
The area of rectangle with PA, PB as sides is equal to the area of square with PC as side
The area of rectangle with PA, PC as sides is equal to the area of square with PB as side
The area of rectangle with PC, PA as sides is equal to the area of square with PA as side
The perimeter of rectangle with PA, PB as sides is equal to the area of perimeter with PC as side
To solve the problem, we need to understand the relationship between the secant and tangent lines to a circle, specifically using the Secant-Tangent Theorem. Here’s a step-by-step solution:
Step 1: Understand the Configuration
We have a circle with a secant line PAB that intersects the circle at points A and B. We also have a tangent line PC that touches the circle at point C.
Hint: Visualize the circle and the lines. Draw the circle and label the points A, B, and C appropriately.
Step 2: Apply the Secant-Tangent Theorem
According to the Secant-Tangent Theorem, the product of the lengths of the segments of the secant line (PA and PB) is equal to the square of the length of the tangent segment (PC). Mathematically, this can be expressed as:
PA×PB=PC2
Hint: Remember that the theorem relates the lengths of the secant and tangent segments.
Step 3: Analyze the Options
Now, we need to analyze the given options based on the theorem:
1. Option A: The area of the rectangle with sides PA and PB is equal to the area of the square with side PC.
- Area of rectangle = PA × PB
- Area of square = PC²
- According to the theorem, PA × PB = PC², so this option is correct.
2. Option B: The area of the rectangle with sides PA and PC is equal to the area of the square with side PB.
- Area of rectangle = PA × PC
- Area of square = PB²
- This does not follow from the theorem, so this option is incorrect.
3. Option C: The area of the rectangle with sides PC and PA is equal to the area of the square with side PA.
- Area of rectangle = PC × PA
- Area of square = PA²
- This does not follow from the theorem, so this option is incorrect.
4. Option D: The perimeter of a rectangle with sides PA and PB is equal to the area of a rectangle with side PC.
- This statement does not relate to the theorem and is not valid.
Hint: Compare the areas and check if they align with the theorem's conclusion.
Step 4: Conclusion
From our analysis, the only correct statement is:
- Option A: The area of the rectangle with sides PA and PB is equal to the area of the square with side PC.
Final Answer: Option A is correct.
We have a circle with a secant line PAB that intersects the circle at points A and B. We also have a tangent line PC that touches the circle at point C.
According to the Secant-Tangent Theorem, the product of the lengths of the segments of the secant line (PA and PB) is equal to the square of the length of the tangent segment (PC). Mathematically, this can be expressed as:
PA×PB=PC2
Now, we need to analyze the given options based on the theorem:
- Area of rectangle = PA × PB
- Area of square = PC²
- According to the theorem, PA × PB = PC², so this option is correct.
- Area of rectangle = PA × PC
- Area of square = PB²
- This does not follow from the theorem, so this option is incorrect.
- Area of rectangle = PC × PA
- Area of square = PA²
- This does not follow from the theorem, so this option is incorrect.
- This statement does not relate to the theorem and is not valid.
From our analysis, the only correct statement is:
- Option A: The area of the rectangle with sides PA and PB is equal to the area of the square with side PC.
Similar Questions
Knowledge Check
Tangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
Let PAB be a secant to a circle intersecting the circle at A and B. Let PT be the tangent segment. If PA = 9 cm and PT =12 cm, then what is AB equal to?
View SolutionBisectors of two adjacent angles A and B of a quadrilateral ABCD intersect each other at a point P. Which one of the following is correct?
View SolutionTangent Secant Theorem
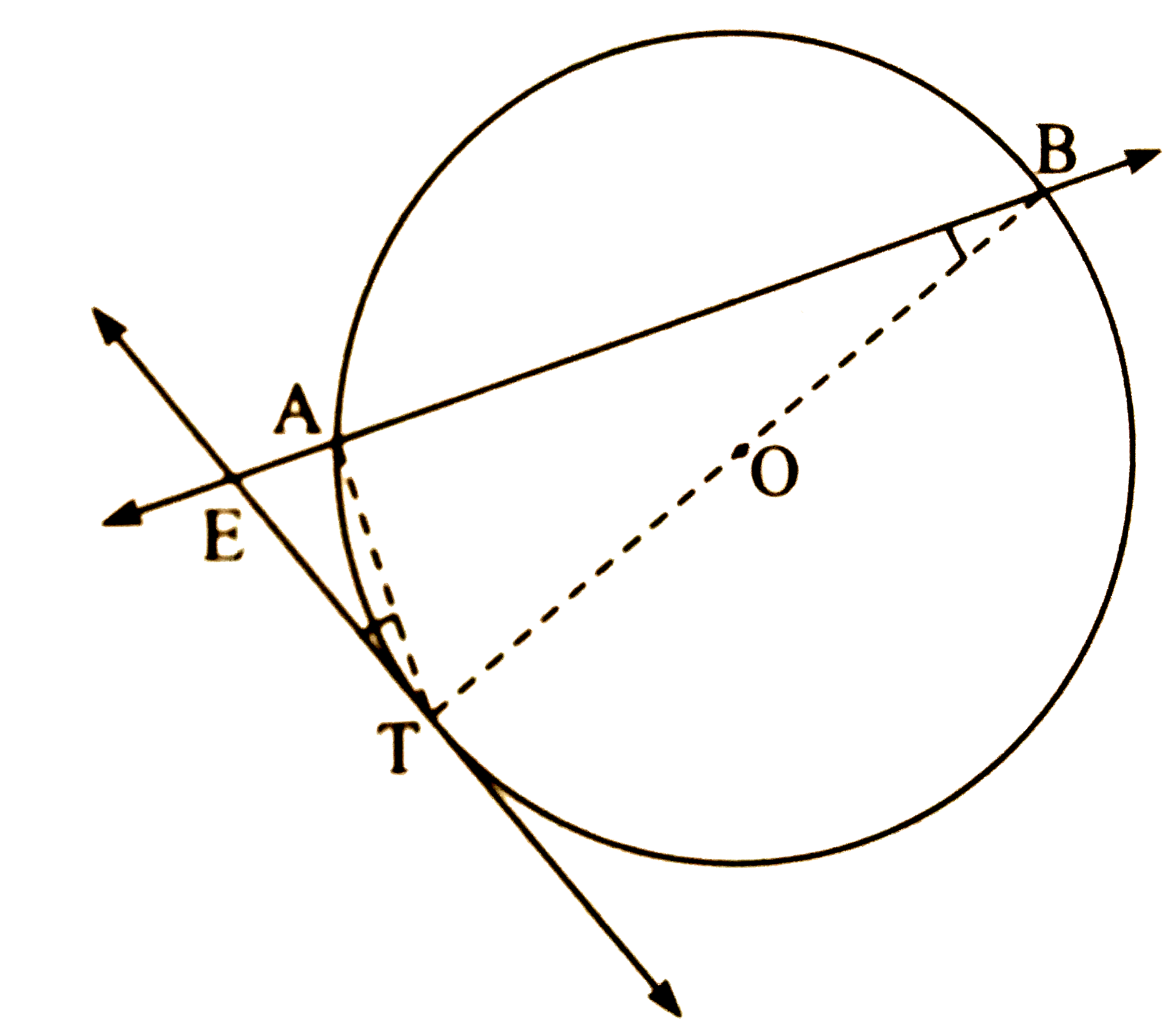
Point E is in the exterior of a circle. A secant through E intersects the circle at points A and B, and a tangent through E touches the circle at point T, then EA×EB=ET2.
Given : (1) A circle with centre O
(2) Tangent ET touches the circle at pointT
(3) Secant EAB intersects the circle at points A and B .
To prove : EA×EB=ET2
View SolutionTwo circles touch each other externally at P. Two secants APB and CPD are drawn through P to meet the circle at A, C and B, D respectively. Then, which one of the following is correct ?
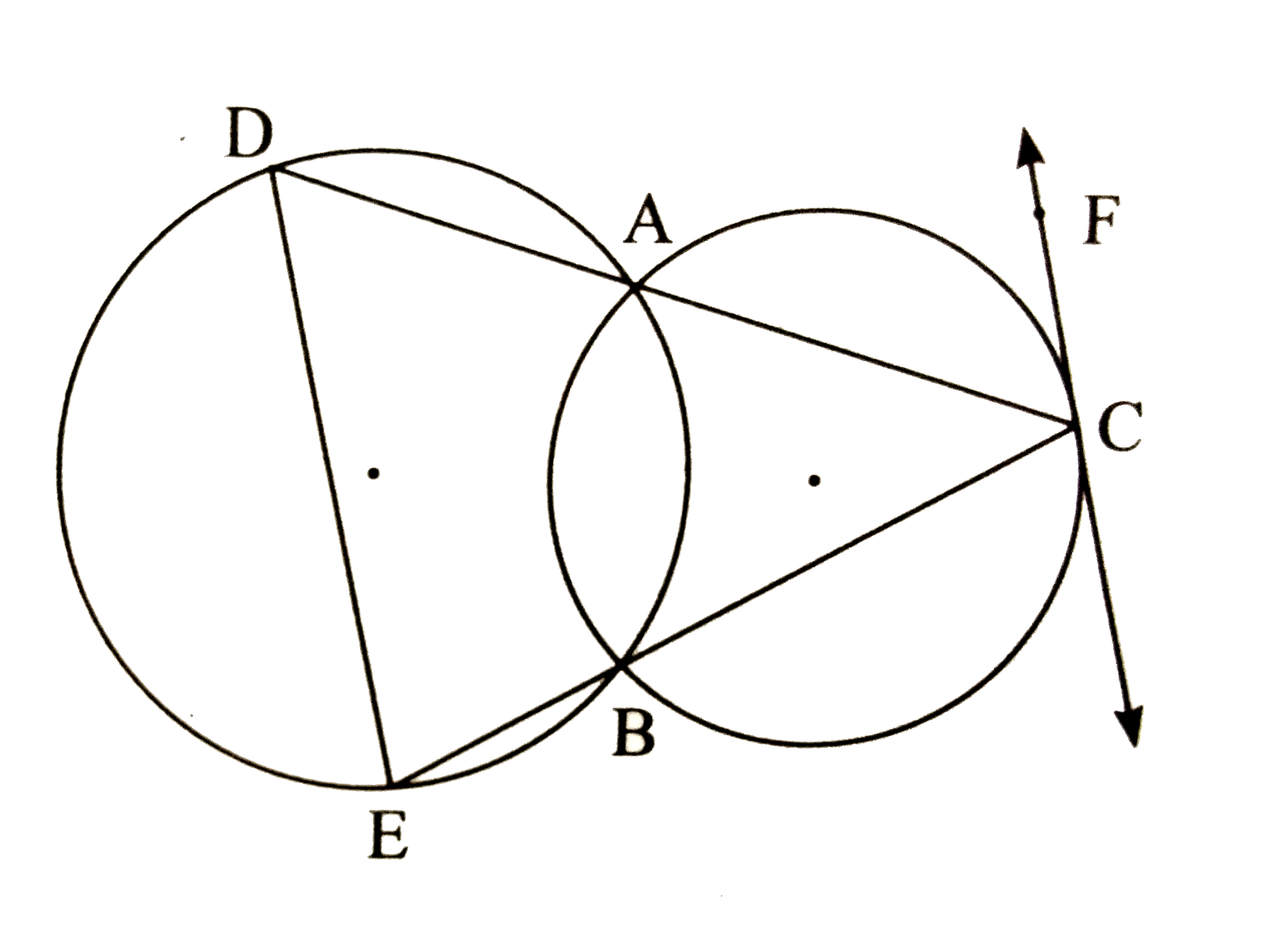
View SolutionIn the figure, two circles intersect each other at points A and B . C is a point on the smaller circle. Secant CA and secant CB of the smaller circle intersect the bigger circle at points D and E respectively then prove : seg DE ∣∣ line CF
View SolutionTANGENT : Intersection point of line and Circle are Coincident.
View SolutionTwo circles with equal radii are intersecting at the points (1,0) and (−1,0). Then tangent at the point (1,0) to one of the circles passes through the centre of the other circle.Then the distance between the centres of these circles is:
View Solution
