A line EF is drawn parallel to the parallel sides AB and CD of a trapezium ABCD where E lies on AD and F lies on BC. If AE:ED=2:1 then what is BF : BC ?
A)2:3
B)3:2
C)2:1
D)1:2
The correct Answer is:A
To solve the problem, we will use the properties of similar triangles and the concept of ratios in trapeziums.
1. Understanding the Trapezium:
- We have a trapezium ABCD with AB || CD (AB is parallel to CD).
- A line EF is drawn parallel to AB and CD, where E lies on AD and F lies on BC.
2. Given Ratio:
- We are given that AE:ED = 2:1. This means if we let AE = 2x, then ED = x.
3. Using Thales' Theorem:
- Since EF is parallel to AB and CD, by Thales' theorem, the segments on the sides AD and BC will be in the same ratio as AE and ED.
- Therefore, we can say that BF:FC = AE:ED = 2:1.
4. Finding BF and BC:
- Let BF = 2y and FC = y (since BF:FC = 2:1).
- Thus, BC = BF + FC = 2y + y = 3y.
5. Finding the Ratio BF:BC:
- Now we can find the ratio BF:BC.
- BF:BC = 2y:3y = 2:3.
6. Final Answer:
- Therefore, the ratio BF:BC is 2:3.
- We have a trapezium ABCD with AB || CD (AB is parallel to CD).
- A line EF is drawn parallel to AB and CD, where E lies on AD and F lies on BC.
- We are given that AE:ED = 2:1. This means if we let AE = 2x, then ED = x.
- Since EF is parallel to AB and CD, by Thales' theorem, the segments on the sides AD and BC will be in the same ratio as AE and ED.
- Therefore, we can say that BF:FC = AE:ED = 2:1.
- Let BF = 2y and FC = y (since BF:FC = 2:1).
- Thus, BC = BF + FC = 2y + y = 3y.
- Now we can find the ratio BF:BC.
- BF:BC = 2y:3y = 2:3.
- Therefore, the ratio BF:BC is 2:3.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B6videos
QUADRILATERAL
- BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B6videos
QUADRILATERAL
- BOOK - LUCENT PUBLICATIONCHAPTER - LINES AND ANGLES EXERCISE - EXERCISE 4B5videos
LINES AND ANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B10videos
TRIGONOMETRIC RATIO OF SPECIFIC ANGLES
Similar Questions
Let AD and BC be the parallel sides of a trapezium ABCD. Let P and Q be the midpoints of the diagonals AC and BD. If AD=16 and BC=20, what is the length of PQ?
View SolutionThe line segments joining the midpoints M and N of parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD=BC
View Solution
Knowledge Check
- Question 1 - Select One
In a trapezium ABCD, where AB||CD and diagonal AC intersects the other diagonal BD at O. If a line segment EF parallel to AB and CD passes through the point O, where E lies on AD and F lies on BC, find the length of EF, provided AB=6 cm and CD = 2 cm.
AA)3 cmBB)4 cmCC)4.5 cmDD)none of these - Question 2 - Select One
In the given figure ABCD is trapezium in which the parallel sides AB and CD both are perpendicular to BC. If AB = 16 m, CD = 8 m and AD = 17 M. What is the area of the trapezium ?
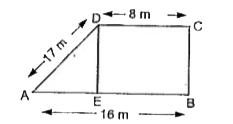 A140 m2B168 m2C180 m2D156.4 m2
A140 m2B168 m2C180 m2D156.4 m2 - Question 3 - Select One
E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
ABCD is a trapezium. Sides AB and CD. are parallel to each other.AB=6 cm, CD=18cm, BC=8cm and AD=12cm. A line parallel to AB divides the trapezium in two parts of equal perimeter. This line cuts BC at E and AD at F. If BE/EC = AF/FD, than what is the value of BE/EC?
ABCD एक सम्लम्ब चतुर्भज है। भुजाएँ AB तथा CD एक दूसरे के समान्तर है। AB=6 सेमी. CD=18 सेमी. BC=8 सेमी. तथा AD= 12 सेमी. है। AB के समान्तर एक रेखा सम्लम्ब को दी बराबर परिमाप वाले हिस्से में काटता है। यह रेखा भुजा BC को E पर तथा AD को F पर काटती है। यदि BE/EC=AF/FD है, तो BE/EC का मान क्या है?View SolutionE and F are respectively the midpoints of the non-parallel sides AD and BC of a trapezium ABCD. Prove that
(i) EF∣∣AB,
(ii) EF=12(AB+CD).View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View SolutionIn the given figure , ABCD is a trapezium in which the parallel sides AB,CD are both perpendicular to BC. Find the area of the trapezium :
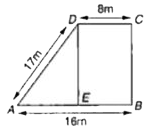 View Solution
View SolutionABC is a triangle and DE is drawn parallel to BC cutting the other sides at D and E. If AB=3.6 cm, AC=2.4 cm and AD=2.1 cm, then AE is equal to :
View Solution

