In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
1:2
1:1
2:3
2:1
The correct Answer is:B
Step by step video, text & image solution for In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B6videos
QUADRILATERAL
- BOOK - LUCENT PUBLICATIONCHAPTER - QUADRILATERAL EXERCISE - Exercise 7B6videos
QUADRILATERAL
- BOOK - LUCENT PUBLICATIONCHAPTER - LINES AND ANGLES EXERCISE - EXERCISE 4B5videos
LINES AND ANGLES
- BOOK - LUCENT PUBLICATIONCHAPTER - TRIGONOMETRIC RATIO OF SPECIFIC ANGLESEXERCISE - Exercise 10B10videos
TRIGONOMETRIC RATIO OF SPECIFIC ANGLES
Similar Questions
Knowledge Check
- Question 1 - Select One
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1 - Question 2 - Select One
ABCD is a parallelogram. BC is produced to Q such that BC = CQ. Then
A(a) area (ΔBCP) = area (ΔDPQ)B(b) area (ΔBCP)> area (ΔDPQ)C(c) area (ΔBCP)< area (ΔDPQ)D(d) area (ΔBCP) + area (ΔDPQ) = area (ΔBCD) - Question 3 - Select One
In parallelogram ABCD, if P is the mid-point of side AB, then
ADP bisects diagonal ACBDP bisects diagonal BDCDP trisects diagonal BDDDP trisects diagonal AC and trisected by AC
ABCD is a parallelogram. E is a point on extended side AB such that AB = BE. By joining D to E it intersects side BC at P. Find length of PC if BC = 15 cm.
View SolutionIn the given figure, Here, ABCD is a parallellogram in which DC is extended to F such that AF intersects BC at E.
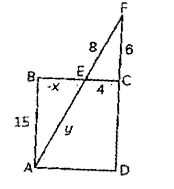
Perimeter of ΔABE=View SolutionABCD is a cyclic quadrilateral. The side AB is extended to E in such a way that BE =BC. If ∠ADC=70∘,∠BAD=95∘, then ∠DCE is equal to
View SolutionIn triangle ABC , sides AB and AC are extended to D and E, respectively, such that AB=BD and AC =CE,F∈dDE,ifBC=6 cm.
View Solutionin ΔABC, a line parallel to side BC cuts the side AB and AC at points D and E respectively and also point D divide AB in the ratio of 1:4. If area of ΔABC is 200 cm2, then what is the area (in cm2) of quadrilateral DECB?
View Solution

